Выпуск: №7(63) КОД науки: исследования молодых ученых

Раздел: Инновационные образовательные технологии

Опубликовано: 14 июня 2024

Код уникальной десятичной классификации: 373.5.016

Автор: Молчева Елена Алексеевна

магистрант 2 курса, Московский городской педагогический университет (МГПУ), г. Москва, e-mail: molchevaea@mgpu.ru

Научный руководитель: Семеняченко Юлия Александровна

доцент департамента математики и физики Института цифрового образования Московского городского педагогического университета (МГПУ)

кандидат педагогических наук, доцент

Аннотация. В статье рассматривается актуальная проблема формирования умения решать задачи по математической грамотности с опорой на метод математического моделирования. Умение составлять математическую модель раскрывает новые возможности в организации учебного процесса, закладывает базу для решения не только стандартных текстовых задач, но и задач по математической грамотности. Приводятся примеры кейсов по математической грамотности, направленных на формирование математической грамотности.

Ключевые слова: математическая грамотность; математическое моделирование; обучающийся, метод-кейс.

Выбор темы данной статьи обусловлен широким использованием в настоящее время математического моделирования в учебном процессе. Умение составлять математическую модель раскрывает новые возможности в организации учебного процесса, закладывает базу для решения задач, а также способствует развитию креативных способностей обучающихся. В современный период развития образования происходит математизация наук, где одним из способов улучшения математического образования является освоение учащимися метода математического моделирования.

По результатам исследования [3] было отмечено, что наибольшие затруднения при решении заданий по математической грамотности обучающиеся испытывали на этапе составления схемы решения задачи и получения уравнения, что свидетельствует о том, что учащимся было трудно произвести грамотный анализ условия задачи и составить математическую модель, которая служит помощником при решении.

В связи с вышеперечисленным возникает следующая задача: научить обучающихся использовать метод математического моделирования при решении задач по математической грамотности.

В статье будет рассмотрена теоретическая сторона данного вопроса, а также приведен ряд кейсов, направленных на применение математического моделирования при решении задач по математической грамотности.

«Математическая грамотность – это способность человека мыслить математически, формулировать, применять и интерпретировать математику для решения задач в разнообразных практических контекстах. Она включает в себя понятия, процедуры и факты, а также инструменты для описания, объяснения и предсказания явлений. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые должны принимать конструктивные, активные и размышляющие граждане в 21 веке» [16].

Анализируя данное определение, можно заметить, что математическая грамотность проверяет способность обучающихся использовать знания из математики для разрешения проблем, возникающих в различных контекстах реального мира: делается акцент не на математических знаниях, а на их применение в практических ситуациях. Следовательно, термин «математическая грамотность» можно охарактеризовать следующими признаками: пониманием роли математики в реальном мире, высказыванием обоснованных математических суждений, использованием математики для разрешения проблем реального мира (см. рисунок 1).

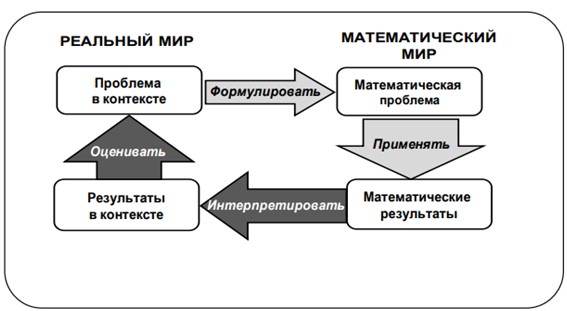
Рис. 1. Модель математической грамотности (PISA)

Проблемные ситуации, рассматриваемые в рамках определенного контекста, являются частью практики участия обучающихся в реальной жизни. Контекст задания – элементы окружающей обстановки, рассматриваемые в рамках конкретной ситуации, взятых из реальной жизни и требующих для своего решения применения математических знаний. Проблемы реального мира представлены в 4 контекстах, являющихся наиболее близкими для обучающихся [16]: общественная жизнь, образование/профессиональная деятельность, научная деятельность.

Задания, проверяющие уровень математической грамотности учеников, включают в себя основные виды проблем, встречающихся в обыденной жизни, которые распределены на следующие категории: пространство и форма, изменение и зависимости, количество, неопределенность и данные.

При решении задач по математической грамотности для описания мыслительной деятельности принято использовать следующие термины [16]:

1. формулировать ситуации математически
   При анализе условия задачи нужно увидеть математическую сущность проблемы, перевести предложенную ситуацию на язык математики, составить математическую модель, отражающую особенности этой ситуации, и найти наиболее легкие способы решения проблемы.

2. применять математику
   При решении задачи ученик должен показать умение применять математические понятия, факты и инструменты как для получения промежуточных решений, так и выводов.

3. интерпретировать
   Данная мыслительная деятельность позволяет перевести математическое решение в контекст реальной проблемы, оценить результат на правдоподобие, то есть позволяет накладывать ограничение в ходе математического решения исходя из условий конкретной ситуации.

4. рассуждать
   Этапы решения задачи включают в себя способность анализировать выдвинутые аргументы и выводы, умение представлять задачу на языке математики, оценивать целесообразность выбранного математического решения, а также способность оценивать и интерпретировать полученные результаты в контексте исследуемой проблемы.

Для того, чтобы разобраться в поставленной задаче статьи, следует обратиться к понятиям математической модели, математического моделирования, а также установить связь этапов математического моделирования с этапами решения задач по математической грамотности

В учебном пособии «основы математического моделирования» С.В. Звонарев приводит определение модели в широком смысле: «материальный или мысленно представляемый объект, который в процессе познания замещает объект – оригинал, сохраняя некоторые важные его черты» [5, с. 9]. Так под моделью в самом широком смысле понимают любой мысленный или знаковый образ моделируемого объекта, именуемого оригиналом.

Классификацию моделей можно проводить по разным критериям. Разберем наиболее практически значимую – распределение по видам средств, применяемых для построения моделей (см. рисунок 2). Выделяют следующие две группы: знаковые и схематизированные, которые в свою очередь также распределяются на подкатегории. Среди схематизированных, которые являются лишь вспомогательными моделями при решении задач, поскольку они выполняют роль перехода от текста задачи к математической модели, выделяют предметные или графические. Предметные модели предполагают физическое взаимодействие с предметами. Графические модели направлены для схематического воссоздания ситуации и их примерами могут служить рисунки и чертежи. Среди знаковых моделей выделяют те, которые выполнены на естественном языке или те, которые выполнены на математическом языке. К знаковым моделям, выполненным на математическом языке, относят выражение, уравнение, запись решения по действиям. Именно они играют главенствующую роль, так как по ним происходит решение задачи.

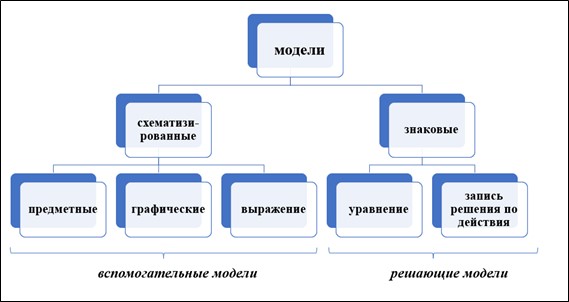
Рис. 2. Классификация моделей по видам средств, применяемых для построения моделей

«Математическая модель – это система уравнений, или арифметических соотношений, или геометрических фигур, или комбинация того и другого, исследование которых средствами математики должно ответить на поставленные вопросы» [8, с. 8]. Таким образом, математическая модель – это совокупность математических зависимостей, которые описывают с определенной степенью точности реальные процессы. Стоит также отметить, что процесс формулировки математической модели называется постановкой задачи.

Под процессом моделирования традиционно понимают изучение с помощью модели соответствующих явлений, процессов, систем объектов, т.е. их оригиналов. Перейдем к понятию «математическое моделирование». Далее будет приведен ряд терминов, раскрывающих суть данного процесса. В статье Н.Е. Ляховой, С.И. Порохни данный термин определяется следующим образом: «Математическое моделирование – описание в виде уравнений и неравенств реальных физических, химических, технологических, экономических, биологических и других процессов». [7, c. 243]. Однако, такая трактовка характерна для текстовых задач, которые решаются алгебраическим способом. С.В. Звонарев определяет математическое моделирование как «идеальное научное знаковое формальное моделирование, при котором описание объекта осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов» [5, c. 23].

Все вышеприведенные определения помогают сделать следующий вывод: математическое моделирование – это описание и представление реального процесса на математическом языке.

Для того, чтобы понять, на какой этап решения задачи следует уделить особое внимание, необходимо сопоставить этапы решения текстовых задач по Л.М. Фридману, выделить этапы решения задач по математической грамотности и этапы процесса математического моделирования. (см. таблицу 1).

Таблица 1. Сравнение этапов решения задачи

№ этапа	Этапы решения задачи согласно определению Л.М. Фридмана	Этапы решения задачи по математической грамотности	Этапы процесса математического моделирования
1 этап	Анализ условия задачи	Анализ проблемной ситуации	Анализ содержания задачи и составление опорных схем, таблиц, чертежей в соответствии с данными условия задачи
2 этап	Схематическая запись условия задачи	Построение математической модели	Построение математической модели
3 этап	Поиск решения задачи	Поиск решения задачи
4 этап	Осуществление решения задачи	Осуществление решения задачи по математической модели	Осуществление решения математической задачи
5 этап	Проверка решения задачи	Проверка решения задачи	Проверка решения
6 этап	Исследование задачи	Интерпретация полученного результата	Интерпретация полученного решения
7 этап	Формулировка ответа задачи	Исследование задачи
8 этап	Анализ решения задачи	Формулировка ответа задачи	Формулирование ответа в соответствии с условием задачи
9 этап		Анализ решения задачи

 

Как можно увидеть из таблицы, выделенных этапов решения задач по математической грамотности больше, чем этапов решения задач по Л.М. Фридману, это связано с тем, что в отличие от традиционных математических задач, при решении задач по математической грамотности обучающемуся необходимо переходить из одного мира в другой (из реального мира в математический мир и наоборот, формулировать возникающие в реальном мире ситуации и переводить их на язык математики, затем разрешать эти ситуации средствами математики, возвращаться с решенной проблемой в реальный мир и интерпретировать полученные математические результаты в реальную жизнь).

Так как наибольшую трудность обучающиеся испытывают непосредственно при составлении математической модели, то необходимо разработать систему заданий, направленную на умение анализировать практическую проблемную ситуацию с последующим составлением математической модели, т.е. такую систему подзадач, которая поможет обучающимся научиться переходить из реального мира в мир математики.

Выделим следующие особенности общепризнанных основных этапов моделирования при обучении математической грамотности:

• Постановка задачи. На текущем этапе требуется выявить проблему в поставленной задаче. Эта проблема должна быть изложена четко и понятно, то есть на простом для учащихся языке. После выделения проблемы задачи необходимо определить объект моделирования, провести его анализ, выявить основные характеристики, элементы и взаимосвязи между ними, а также определить результат.
• Разработка математической модели. Целью данного этапа является отбор данных, необходимых для построения модели, с последующим преобразованием словесного описания в модель, описанной математическим языком.
• Реализация математической модели. На данном этапе происходит разработка математического метода решения сформулированной на языке математики задачи.
• Планирование вычислительного эксперимента и анализ результатов эксперимента. На этом этапе определяют, какие параметры модели и в каких пределах можно их изменять при проведении вычислительного эксперимента.

Главным, чему следует учить в современном мире – умение осваивать и использовать новую информацию для решения стоящих перед человеком задач. Для достижения новых результатов образования необходимо использовать эффективные методы, один из них – это кейс-метод. Это метод, позволяющий субъектам жизнедеятельности, общения, познания осмысливать реальные жизненные проблемы и ситуации с целью их преобразования.

Кейс-метод – это метод активного обучения на основе реальных ситуаций, которые преподносятся обучающимся в виде микропроблем [1, с. 105-111]. При этом знания приобретаются в процессе активного поиска разрешения проблем. Кейс состоит из описания реальных событий, описание может быть представлено с помощью слов, картинок, схем, чертежей. Кейс фиксирует динамику ситуации, процесса в конкретных временных пределах, дает возможность обучающимся выявить проблему, осуществить выбор путей и способов ее решения, актуализировать необходимый для ее решения опыт. Этим кейс отличается от математической текстовой задачи: он не предлагает проблему для решения явно, ее необходимо увидеть, перефразировать в математический вопрос.

Кейс-метод наиболее удачно позволяет интегрировать возможности математического моделирования при решении задач на математическую грамотность: каждый этап математического моделирования сопоставляется с мыслительными операциями, использующимися при решении задач по математической грамотности. Кейс представляет собой комплекс заданий, связанных одной тематикой, следовательно, решение кейсов по математической грамотности может охватить все мыслительные операции, которые используются при решении заданий по математической грамотности: формулировать ситуации на языке математики, применять математику, интерпретировать результат, рассуждать.

Рассмотрим разработанный кейс по математической грамотности, при решении которого используется математическое моделирование.

КЕЙС «Увлечения домохозяйки Наташи»

Уважаемые ученики! Работая с кейсом «Увлечения домохозяйки Наташи», вы научитесь применять математику в совсем обычных для многих ситуациях, интерпретировать полученные результаты в ограниченных условиях, анализировать свою работу, сделанный выбор.

Цель вашей работы – умение находить оптимальное значение величин, моделировать оптимальные варианты упаковки товара, рассчитывать выручку, применять эти умения в жизненных ситуациях.

Задачи:

• научиться анализировать условия с точки зрения ограничений по различным параметрам;
• научиться по данным условиям искать оптимизируемую величину;
• научиться искать выручку от продажи товара по незаданной цене и количеству товара;
• научиться влиять на ход событий с помощью математики.

Вводная часть
Наталье Михайловне 28 лет и она успешная домохозяйка, замужем. Её увлечения – это скрапбукинг, вязание и просмотр сериалов по телеканалу «России 1», которые обычно начинаются в 20:45.

Ситуация 1
Муж Натальи Серафим взял двухнедельный отпуск на работе. После некоторого отдыха дома молодому семейству захотелось привнести активность в жизнь. Они решили съездить за грибами в лес, который находится в Серпуховском районе Подмосковья. Там находится загородный дом их друзей.

Вопрос 1. Наталья заволновалась – успеют ли они вернуться до начала сериала? Как Серафиму успокоить жену?
Подсказка: Используйте координатную плоскость и приложение для построения графиков.

Ситуация 2
По возвращении в дом друзей пара обнаружила, что те разбирают разные ненужные вещи. Наталья заметила поролоновые куски, которые были в хорошем состоянии и ей пришла идея: сделать из них шарики для стирки (см. рисунок 3). Попытки очистить одежду от шерсти увенчались успехом, и Наталья решила начать зарабатывать на изготовлении такого товара.

Рис. 3. Шарики для стирки

Задание 2. Проанализировав за месяц рынок аналогичных товаров Наталья пришла к выводу, что функция спроса чаще всего выражается следующим образом: q = 100 – p, где q – количество товара, p – цена за единицу товара.
Вопрос 2. Наталья хочет иметь максимальную выручку от своей работы. Помогите ей разобраться, как это сделать.
Справочный материал:
* Спрос – это зависимость между ценой товара и количеством, которое покупатель может и хочет приобрести на рынке в течение определенного времени.
* Выручка – это доход от реализации товаров, работ или услуг.

Ситуация 3
Бизнес Натальи начал стремительно развиваться. И ей пришла идея продавать шарики для стирки не поштучно, а комплектом. Для этого нужна упаковка.
Задание 3. Самый выгодный вариант – заказывать картонные листы размером 60 см Х 60 см и из них делать коробки, которые будут (по правилам) затягиваться производственным полиэтиленом на складе площадки. Было принято решение делать квадратные картонные коробки без крышки.
Вопрос 3. Подскажите Наталье, как сделать самую вместительную упаковку.

Завершающая часть
Уважаемые ученики! При выполнении заданий кейса «Увлечения домохозяйки Наташи»:
вы узнали: что такое оптимизируемая величина и как она может влиять на ход событий и различные реальные ситуации;
вы научились: решать задачи на оптимизацию;
теперь вы можете: применять умение решать задачи на оптимизацию при поиске необходимой информации, находить вариант ответа, который подходит наилучшим образом.

Решение кейса по математической грамотности в рамках понятий математического моделирования

Задание 1
Постановка задачи. На первом этапе необходимо найти проблему. По условию задачи обучающимся необходимо узнать, сможет ли семейная пара вернуться с прогулки до начала сериала. Так как сериал начинается в 20:45, значит для того, чтобы узнать, успеет ли Наташа вернуться к началу сериала, необходимо узнать, во сколько пара окажется дома. Математический вопрос поставлен: во сколько Наташа с Серафимом придут домой после прогулки?

Разработка математической модели. Представленная ситуация описана словесной формой, следовательно, обучающимся необходимо вспомнить знания, полученные на уроках математики, которые могли бы натолкнуть на правильный метод решения, который поможет справиться с возникшей жизненной ситуацией: необходимо изобразить маршрут пары (см. рисунок 4). Пусть пара находится в точке А от дороги они отошли на 5 км, значит точка С находится в 5 км от точки А (пара шла по прямой), дом друзей находится в 13 км от пары (точка В). Далее следует поразмышлять, по какому пути паре следует возвращаться домой: движение по лесу медленнее движения по дороге, значит, если идти напрямую к дому друзей через лес, то это вариант не сэкономит время. Идти по лесу до дороги, а оставшееся расстояние по дороге до дома друзей тоже долго (так как проходится большее расстояние по дороге и большее расстояние по лесу). Поэтому можно «срезать» через лес часть пути.

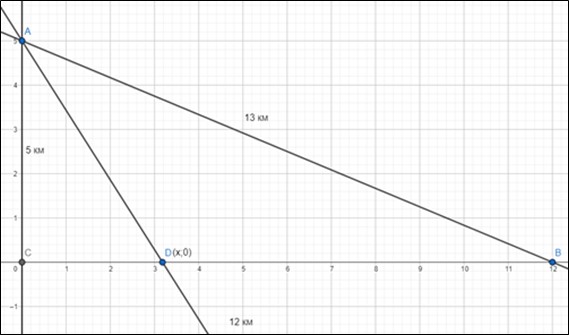
Рис. 4. Маршрут семейной пары 

Реализация математической модели. На этом этапе ученики используют полученные раннее математические знания: проведение различных вычислительных процедур, в частности, нахождение наибольшего/наименьшего значения функции, нахождение экстремумов функции.

Подставив в исходную функцию значение х, получим примерное время 3 часа 44 минуты.

Планирование вычислительного эксперимента и анализ результатов эксперимента. На данном этапе ученики получают ответ сформулированной самостоятельно математической задачи, т.е. поднимающаяся проблема задачи по математической грамотности еще не разрешена, необходимо перевести ответ, полученный в математической задаче, в реальный мир. Ученики должны ответить на вопрос: успеет ли семейная пара вернуться до начала сериала. Так как в математической задачи был получен ответ 20:44, а сериал начинается в 20:45, то Наташа с мужем успеют вернуться домой до начала сериала.

Ответ: пара вернется домой в 20:44, а значит, успеет вернуться до начала сериала.

Задание 2
Постановка задачи. На данном этапе необходимо перевести вопрос, поставленный в рамках реальной жизненной ситуации, на язык математики, т.е. сформулировать математический вопрос задачи. Необходимо узнать, при подстановке какой цены товара и какого количества товара в найденную Наташей функцию получится максимальная выручка.

Разработка математической модели. По условию задачи функция спроса выражается следующим образом: q = 100 – p, где q – количество товара, p – цена за единицу товара. По определению выручка будет рассчитываться как произведение стоимости товара на количество.
То есть выручка y=(100-p)×p. Проанализируем выручку, как функцию y = –p² + 100 p.

Разработка математической модели. По условию задачи функция спроса выражается следующим образом: , где  – количество товара,  – цена за единицу товара. По определению выручка будет рассчитываться как произведение стоимости товара на количество. То есть выручка . Проанализируем выручку как функцию .

Реализация математической модели.  – квадратичная функция, перед старшей степенью стоит отрицательный коэффициент. Значит, ветви графика функции направлены вниз, поэтому максимальное значение функции достигается в вершине параболы. Координата вершины  (). Найдем значение функции в точке , получаем .

Планирование вычислительного эксперимента и анализ результатов эксперимента. Так как квадратичная функция, ветви графика которой направлены вниз, достигает своего наибольшего значения в вершине, то при цене будет достигаться максимальная выручка. При такой стоимости Наташа может продать  товара, а выручка составит

Ответ: Наташа получит максимальную выручку 2500 рублей при продаже 50 штук товара по 50 р/шт.

Задание 3
Постановка задачи. По условию представленной задачи необходимо найти самую вместительную упаковку, то есть такую упаковку, в которую поместится наибольшее количество продаваемого товара. Значит, нужно найти размеры коробки, объем которой будет наибольший.

Разработка математической модели. Сначала нужно определить, как сложить коробку из квадратного листа. Если по краям вырезать квадраты, то можно сложить коробку (см. рисунок 5). Обозначим стороны вырезанного квадрата за , именно их и нужно будет найти, тогда получим, что стороны необходимой коробки будут по  (лист картона имеет размер , с каждой стороны вырезаем квадраты по , тогда оставшаяся часть картонного листа будет иметь размер , высота коробки - ). Так как по условию нужна коробка с наибольшим объемом, то составим формулу для нахождения объёма квадратной коробки с заданными измерениями: . Нужно определить границы изменения переменной  и сформулировать математическую постановку задачи. Так как сторона квадрата равна 60 см, то с обеих сторон можно отрезать части длиной от 0 до 30 см, т.е. .

 

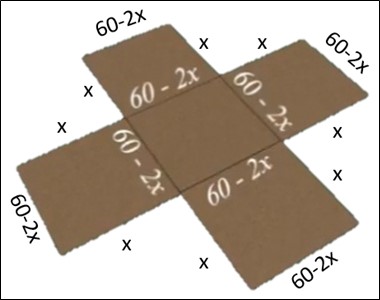
Рис. 5. Макет коробки

Ответ: Если вырезать квадраты , то коробка будет самой вместительной.

Таким образом, этапы моделирования напрямую связаны с мыслиительными операциями, применяемыми при решении заданий по математической грамотности: постановка задачи – формулировать задачу на языке математики, разработка и реализация математической модели – применять математику, планирование вычислительного эксперимента и анализ результатов эксперимента – интерпретировать и оценивать. Использование математического моделирования позволяет учащимся увидеть связь между математическими понятиями и реальными ситуациями, что помогает им лучше понимать суть задач и применять математику в повседневной жизни. Кроме того, работа с математическими моделями развивает умение анализировать данные, делать выводы и принимать решения на основе математических суждений.

Использование кейсов при обучении математической грамотности даёт учащимся возможность овладеть навыками анализа ситуаций, планирования своих действий, моделирования решения. Приведенный в статье кейс содержит все этапы математического моделирования, которые были подробно разобраны в работе. При решении задач по математической грамотности метод-кейс позволяет увидеть применение математики в реальном мире, объединяя в себе несколько проблемных ситуаций, связанных одной тематикой, решение которых достигается посредством применения метода математического моделирования.

Список литературы:

1. Атласова А.Д. Использование кейс-технологии в образовательном процессе // Дистанционное и виртуальное обучение. 2010. №11(41). C. 105-111.
2. Боровских А.В. О понятии математической грамотности // Педагогика. 2022. Т. 86. №3. С. 33-45.
3. Васильева Р.Л., Тяглова Е.Г. Формирование математической грамотности на уроках (из опыта работы творческой группы учителей Красноярского края): методические рекомендации. Красноярск, 2022. 94 с. (дата обращения: 03.02.2024).
4. Зайцева Н.А. Математическое моделирование. М.: Институт транспортной техники и систем управления, 2017. 110 с.
5. Звонарев С.В. Основы математического моделирования: учебное пособие. Екатеринбург: Изд-во Урал. ун-та, 2019. 112 с.
6. Лукичева Е.Ю. Математическая грамотность: обзор понятия и методики формирования // Непрерывное образование. - 2020. - № 3. - С. 46-53. (дата обращения: 15.02.2024).
7. Ляхова Н.Е., Порохня С.И. Обучение элементам математического моделирования в процессе решения текстовых задач // Таганрогский государственный педагогический университет им. А.П. Чехова (Таганрог). 2017. С. 243-248.
8. Мышкис А.Д. Элементы теории математических моделей. М.: Ленанд, 2019. 304 с.
9. Особенности формирования и оценки математической грамотности школьников / Л.О. Денищева, Н.В. Савинцева, И.С. Сафуанов, А.В. Ушаков, В.А. Чугунов, Ю.А. Семеняченко // Вестник НГПУ. 2021. №4. (дата обращения: 19.02.2024).
10. Рослова Л.О. Концептуальные основы формирования и оценки математической грамотности / Л.О. Рослова, К.А. Краснянская, Е.С. Квитко // Отечественная и зарубежная педагогика. 2019. Т. 1, №4(61). С. 58-79. (дата обращения: 17.12.2023).
11. Рослова Л.О. Проблема формирования способности «применять математику» в контексте уровней математической грамотности / Л.О. Рослова и др. // Отечественная и зарубежная педагогика. 2020. Т. 2. №2(70). С. 74-99.
12. Рослова Л.О. Функциональная математическая грамотность: что под этим пониматьи как формировать // Педагогика. 2018. №10. С. 48-55. (дата обращения: 09.02.2024).
13. Универсальные компетентности и новая грамотность: чему учить сегодня для успеха завтра. Предварительные выводы международного доклада о тенденциях трансформации школьного образования / И.Д. Фрумин, М.С. Добрякова, К.А. Баранников, И.М. Реморенко // Нац. исслед. ун-т «Высшая школа экономики». Институт образования. М.: НИУ ВШЭ, Современная аналитика образования. 2018. №2(19). 28 с.
14. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Кн. для учащихся ст. классов сред. шк. 3-е изд., дораб. М.: Просвещение, 1989. 192 с.
15. Функциональная грамотность: глобальные компетенции: Отчет по результатам международного исследования PISA-2018. (дата обращения: 26.02.2024)
16. PISA 2021. Mathematics Framework (Second Draft). (дата обращения: 12.02.2024).

The importance of mathematical modeling in teaching mathematical literacy problem solving

Molcheva E.A.,
undergraduate of 2 course of the Moscow City University, Moscow

Research supervisor:
Semenyachenko Julia Alexandrovna,
Associate Professor of the Department of Mathematics and Physics of the Institute of Digital Education of the Moscow City University. Candidate of Pedagogical Sciences, Associate Professor

Abstract. The article deals with the actual problem of the formation of the ability to solve problems in mathematical literacy based on the method of mathematical modeling. The ability to make a mathematical model opens up new opportunities in the organization of the educational process, lays the foundation for solving not only standard text problems, but also problems in mathematical literacy. Examples of mathematical literacy cases aimed at the formation of mathematical literacy are given.
Keywords: mathematical literacy; mathematical modeling; student, method-case.

References:

1. Atlasova A.D. The use of case technology in the educational process // Distance and virtual learning. 2010. №11(41).: 105-111.
2. Borovskikh A.V. On the concept of mathematical literacy // Pedagogy. 2022. Vol. 86. №: 33-45.
3. Vasilyeva R.L., Tyaglova E.G. Formation of mathematical literacy in the classroom (from the experience of the creative group of teachers of the Krasnoyarsk Territory): methodological recommendations. Krasnoyarsk, 2022. 94 p. (date of the address: 03.02.2024).
4. Zaitseva N.A. Mathematical modeling. Moscow: Institute of Transport Engineering and Control Systems, 2017. 110 p.
5. Zvonarev S.V. Fundamentals of mathematical modeling: a textbook. Yekaterinburg: Ural Publishing House. University, 2019. 112 р.
6. Lukicheva E.Y. Mathematical literacy: an overview of the concept and methodology of formation // Continuing education. 2020. №3.: 46-53. (date of the address: 15.02.2024).
7. Lyakhova N.E., Porokhnya S.I. Teaching elements of mathematical modeling in the process of solving text problems // Taganrog State Pedagogical University named after A.P. Chekhov (Taganrog). 2017.: 243-248.
8. Myshkis A.D. Elements of the theory of mathematical models. Moscow: Lenand, 2019. 304 p.
9. Features of the formation and assessment of mathematical literacy of schoolchildren / L.O. Denishcheva, N.V. Savintseva, I.S. Safuanov, A.V. Ushakov, V.A. Chugunov, Yu.A. Semenyachenko // Bulletin of NGPU. 2021. №4. (date of the address: 19.02.2024).
10. Roslova L.O. Conceptual foundations of the formation and assessment of mathematical literacy / L.O. Roslova, K.A. Krasnyanskaya, E.S. Kvitko // Domestic and foreign pedagogy. 2019. Vol. 1, №4(61).: 58-79. (date of the address: 17.12.2023).
11. Roslova L.O. The problem of forming the ability to «apply mathematics» in the context of levels of mathematical literacy / L.O. Roslova et al. // Domestic and foreign pedagogy. 2020. Vol. 2. №2(70).: 74-99.
12. Roslova L.O. Functional mathematical literacy: what is meant by this and how to form // Pedagogy. 2018. №10.: 48-55. (date of the address: 09.02.2024).
13. Universal competencies and new literacy: what to teach today for tomorrow's success. Preliminary conclusions of the international report on trends in the transformation of school education / I.D. Frumin, M.S. Dobryakova, K.A. Barannikov, I.M. Remorenko // National research. Higher School of Economics, Institute of Education, Moscow, Higher School of Economics. Modern Education Analytics,№2(19). 28 p.
14. Friedman L.M., Turetsky E.N. How to learn to solve problems: A book for students of art classes of secondary schools. 3rd ed., dorab. Moscow: Enlightenment, 1989. 192 p.
15. Functional literacy: Global competencies: A report on the results of the PISA-2018 international study. (date of the address: 26.02.2024).
16. PISA 2021. Mathematics Framework (Second Draft)]. (date of the address: 12.02.2024).