Аннотация. В настоящей работе предложены пути внедрения планиметрических задач в школьный курс алгебры и начал анализа при изучении темы «Наибольшее и наименьшее значение функции». Авторами предложены и решены задачи с методическими рекомендациями к их применению в процессе обучения математике в 10-11 классах.
Ключевые слова: дифференциальное исчисление функции одного переменного, производная, алгебра и начала математического анализа, планиметрические задачи, наибольшее (наименьшее) значение функции.
Аппарат математического анализа чрезвычайно активно используется в самых разнообразных разделах науки, понятия, свойства и теоремы математического анализа помогают моделировать и дают возможность разрешать множество практических ситуаций.
В большинстве школьных учебников представлены задачи, для решения которых ученику достаточно только лишь воспроизводить известный алгоритм нахождения наибольшего (наименьшего) значения функции. Безусловно, такие задания необходимы на первом этапе изучения новой темы, ведь именно такие задачи позволяют выработать навык нахождения наибольшего (наименьшего) значения функции. Однако, ограничиваясь лишь данными заданиями, учитель теряет замечательную возможность построить метапредметные связи во время урока, ведь данная тема, как нельзя лучше, позволяет рассматривать межпредметные задачи на уроках математики, что способствует поддержанию познавательного и исследовательского интереса учащихся, мотивирует их находить связи и закономерности математики и других областей наук.
К сожалению, в рамках школьного курса алгебры и начал математического анализа из-за различных причин не хватает внимания задачам из прочих научных областей, особенно планиметрии. Однако внедрение в учебный план таких задач может дать следующие преимущества:
- улучшить понимание связей между курсами алгебры и математического анализа для 10-11 классов и планиметрией для 7-9 классов;
- продемонстрировать применение дифференциального исчисления для решения планиметрических задач;
- показать применение дифференциального исчисления при решении задач оптимизации;
- подчеркнуть, что дифференциальное исчисление играет важную роль в решении некоторых планиметрических задач;
- повысить готовность учащихся к сдаче ЕГЭ по профильной математике.
Как уже упоминалось, сфера применения математического анализа весьма обширна, но в этой статье мы рассмотрели его применение в области планиметрии. Ниже приведен пример алгоритма решения задач на оптимизацию:
- Проанализировать условие задачи и выделить оптимизируемую величину (обозначить как .
- Ввести переменную x, которая будет обозначать неизвестное значение, от которого напрямую зависит оптимизируемая величина.
- Установить границы числового промежутка, в пределах которого может варьироваться введенная переменная.
- Выразить все необходимые неизвестные величины, которые требуются для задания функции, через переменную x и численные данные задачи, подставив их в формулу функции.
- Определить, каким образом необходимо оптимизировать полученную функцию и в каких пределах это делать.
- Следуя алгоритму нахождения наибольшего или наименьшего значений функции, вычислить искомое значение.
Перейдем непосредственно к рассмотрению конкретных задач.
Задача 1. Найдите наибольшую площадь прямоугольника, вписанного в окружность радиуса 5 (см. рисунок 1).
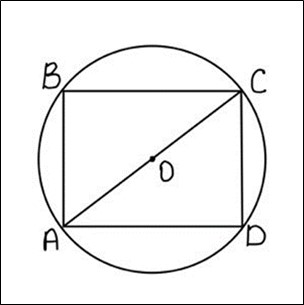
Рис. 1. Чертеж к задаче 1

Задача 2. Дана равнобедренная трапеция с площадью S и высотой h (см. рисунок 2). Каким должен быть угол между боковой стороной и основанием, чтобы сумма длин меньшего основания и боковых сторон трапеции была наименьшей?
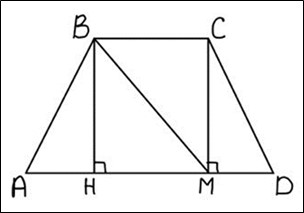
Рис. 2. Чертеж к задаче 2

Задача 3. Найдите стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R (см. рисунок 3).
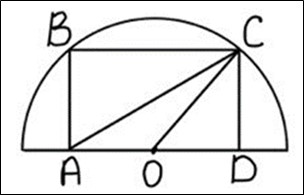
Рис. 3. Чертеж к задаче 3

Задача 4. Дан прямоугольник, завершенный сверху полукругом. Периметр этой фигуры равен P (см. рисунок 4). Определите, при каких линейных размерах, площадь фигуры будет наибольшей.
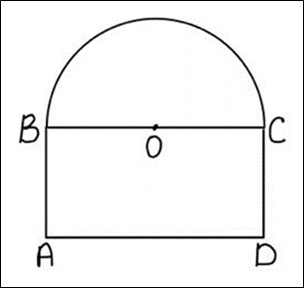
Рис. 4. Чертеж к задаче 4

Вывод. Авторы статьи постарались показать, что внедрение задач такого типа в курс алгебры и начал анализа позволяет обучающимся увидеть широту применения аппарата математического анализа при решении задач из смежных областей (планиметрии). Кроме того, такие задачи можно считать исследовательскими, так как при их решении учащимся приходится устанавливать связи между различными геометрическими фигурами на плоскости. Задачи можно легко включить в учебный процесс по алгебре и началам анализа, поскольку по сути от учащихся требуется решить задачу на поиск максимального (минимального) значения функции.
Список литературы:
- Корешкова Т.А., Семеняченко Ю.А. Математический анализ. Дифференциальное и интегральное исчисление функции одной переменной: учебно-методическое пособие для самостоятельной работы студентов педагогических вузов. М.: МГПУ, 2011. 164 с.
- Савватеев Д.А., Мошенина Е.Д. Применение дифференциального исчисления функции одного переменного при решении задач школьного курса стереометрии // Наука в Мегаполисе Science in a Megapolis. М.: 2023. №3(48). (дата обращения: 01.02.2024).
- Сборник задач по математике для поступающих в вузы / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; Под ред. М.И. Сканави. 6-е изд. М.: Мир и Образование, 2019. 608 с.
- Улимаева А.Т. Роль и место задач на оптимизацию в обучении математике: диссертация на соискание ученой степени кандидата педагогических наук. Москва, 1977. 272 с.
Introduction of planimetric problems in the school course of algebra and the principles of analysis
Moshenina E.D.,
bachelor of 4 course of the Moscow City University, Moscow
Coauthor:
Savvateev D.A.,
bachelor of 4 course of the Moscow City University, Moscow
Abstract. In this article, the ways of introducing planimetric problems into the school course of algebra and the principles of analysis in the study of the topic «The largest and smallest value of a function» are proposed. The authors proposed and solved problems with methodological recommendations for their application in the process of teaching mathematics in grades 10-11.
Keywords: differential calculus of a function of one variable, derivative, algebra and the beginning of mathematical analysis, planimetric problems, the largest (smallest) value of the function.
References:
- Koreshkova T.A., Semenyachenko Yu.A. Mathematical analysis. Differential and integral calculus of a function of one variable: an educational and methodical manual for independent work of students of pedagogical universities Moscow: MSPU, 2011. 164 p.
- Savvateev D.A., Moshenina E.D. Application of differential calculus of a function of one variable in solving problems of the school course of stereometry // Science in a Megapolis Science in a Megapolis. Moscow: 2023. №3(48). (date of the address: 01.02.2024).
- Collection of problems in mathematics for university applicants / V.K. Egerev, V.V. Zaitsev, B.A. Kordemsky, etc.; Edited by M.I. Skanavi. 6th ed. Moscow: World and Education, 2019. 608 p.
- Ulimaeva A.T. The role and place of optimization tasks in teaching mathematics: dissertation for the degree of Candidate of Pedagogical Sciences. Moscow: 1977. 272 p.
