Аннотация. В данной статье рассматривается реализация межпредметных связей с геометрией на занятиях по робототехнике. Анализируются некоторые задания школьного этапа Всероссийской олимпиады школьников по робототехнике для 7-8 классов. Показывается, как может осуществляться подготовка к выполнению данного рода заданий на занятиях по робототехнике.
Ключевые слова: робототехника, геометрия, межпредметная связь, олимпиада.
Робототехнике в современном мире уделяется повышенное внимание во многих сферах деятельности человека: промышленность, банковское обслуживание, медицина, образование, сфера развлечений и т.д. [2, с. 39].
На производстве применение роботов позволяет избавить человека от тяжелой и порой опасной работы. В повседневной жизни роботы-помощники (например, робот-няня, робот-ассистент, робот-уборщик) позволяют удовлетворять каждодневные потребности людей. Постепенно робототехника будет гармонична связана со всеми сферами нашей жизнедеятельности. Поэтому подготовка высококвалифицированных специалистов в данном направлении – актуальная задача современного общества [4, с. 92-93].
У образовательных учреждений имеется значительный интерес к дисциплинам инженерно-технической направленности: 3D-моделирование, прототипирование, электроника, робототехника [1, с. 53].
Обучение робототехнике уже осуществляется в школах, где учащиеся конструируют и программируют различных роботов с использованием специальных робототехнических конструкторов (Lego Mindsrorm, VEX Robotics, Роботрек и др.) [3, с. 41].
Особенностью данного направления, является межпредметность, т.е. связь с такими предметами школьной программы, как «Математика», «Физика», «Информатика». Без базовых знаний по данным дисциплинам невозможно дальнейшее освоение робототехники [3, с. 41].
Продемонстрировать свои знания и умения по робототехнике ученики могут на различных олимпиадах, выставках, робототехнических соревнованиях. И без знаний из других школьных дисциплин на таких мероприятиях просто не обойтись.
В данной статье уделено особое внимание такому разделу математики, как геометрия. Проанализируем несколько заданий школьного этапа Всероссийской олимпиады школьников по робототехнике на 2020-2021 год для 7-8 классов [5].
Задача 1. Саша выполнил чертёж и нанёс на него размеры в сантиметрах (рис. 1). Определите, чему равен периметр данной фигуры. Ответ дайте в дециметрах. В ответ запишите только число (см. рисунок 1).
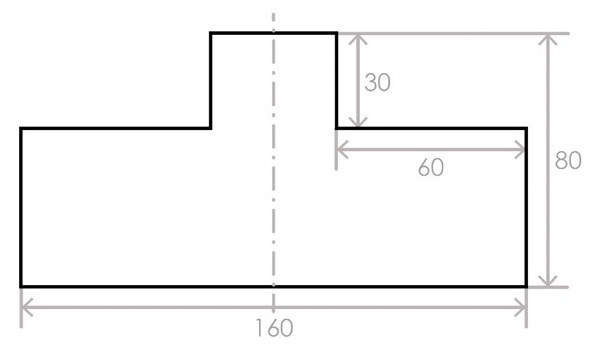
Рис. 1. Чертёж
Чтобы верно выполнить данное задание, ученику необходимо увидеть, что заданную фигуру можно достроить до прямоугольника, либо разбить ее на три прямоугольника. И, соответственно, периметр фигуры будет равен периметру получившегося прямоугольника, либо сумме периметров трех прямоугольников. Следовательно, чтобы решить данное задание, ученик должен знать следующие темы по геометрии:
- Отрезок. Длина отрезка
- Прямоугольник. Формула периметра прямоугольника.
На занятиях по робототехнике можно сконструировать и запрограммировать робота, двигающегося по такому чертежу и определяющего периметр получившейся фигуры. Таким образом, у учеников возникнет мотивация к изучению основ геометрии, и появится возможность применить эти знания на практике посредством робототехники.
Задача 2. В комплект робототехнического полигона входят горки пяти типов. Все горки выполнены из одного материала (см. таблицу 1). Определите, по горке какого типа роботу будет проще всего подняться наверх.
Таблица 1. Параметры горок
| Тип горки | Количество (шт.) | Длина основания горки (дм.) | Высота горки (см.) |
|---|---|---|---|
| А | 3 | 10 | 40 |
| В | 2 | 12 | 40 |
| С | 2 | 8 | 40 |
| D | 1 | 7 | 40 |
| Е | 1 | 4 | 40 |
В данном задании ученику понадобятся знания по теме «Соотношение между сторонами и углами прямоугольного треугольника». Чем больше угол наклона горки, тем сложнее будет подниматься по ней роботу. Значит, необходимо выбрать ту горку, у которой угол наклона меньше всех.
Горка на чертеже может быть представлена в виде прямоугольного треугольника. Тогда для того, чтобы найти угол наклона, нужно вычислить тангенс этого угла для каждой горки и выбрать среди полученных значений наименьшее. Тангенс угла наклона в данном случае будет равняться отношению высоты горки к длине ее основания.
На занятиях по робототехнике подготовка к решению такого рода задач помогает ученикам освоить одну из проблемных тем геометрии. Это можно осуществить посредством эксперимента. Сделать горки с заданными параметрами длины и высоты из какого-нибудь материала (картона, пластика, древесины). Сконструировать простого робота, осуществляющего движение. Выяснить, по какой горке робот поднимается быстрее всего. Обсудить с учителем, от каких параметров горки это зависит.
Таким образом, робототехника позволяет ученикам экспериментальным путем изучить соотношение между сторонами и углами прямоугольного треугольника.
Задача 3. Робот-чертёжник движется по ровной горизонтальной поверхности и наносит на неё изображение (см. рисунок 2) при помощи кисти, закреплённой посередине между колёс. Из-за крепления кисти робот не может ехать назад. Все повороты робот должен совершать на месте, вращая колёса с одинаковой скоростью в противоположных направлениях.
Робот должен нарисовать треугольник. Углы данного треугольника равны 30°, 60° и 90°. Робот оснащён двумя отдельно управляемыми колёсами, расстояние между центрами колёс составляет 50 см, радиус колеса робота 10 см, максимальная скорость вращения моторов 2 оборота в секунду. Определите, на какой минимальный суммарный угол должен повернуться робот, чтобы начертить данную фигуру.
При расчётах примите π ≈ 3. Ответ дайте в градусах. В ответ запишите только число.
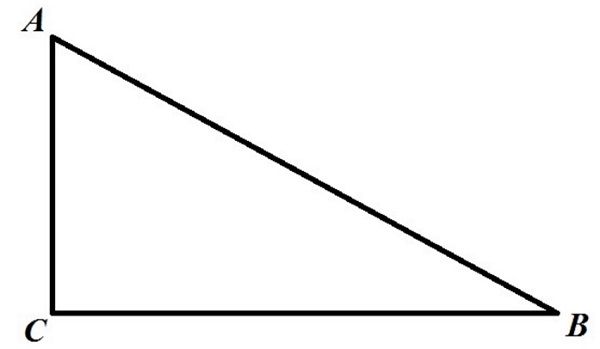
Рис. 2. Траектория
Чтобы начертить данную фигуру, робот должен проехать три прямолинейных участка. При этом поворот будет производиться всего два раза (в двух вершинах треугольника), так как на исходном и конечном пунктах поворот не требуется. При этом угол поворота робота будет равняться величине смежного угла для угла с соответствующей вершиной треугольника. Сумма смежных углов равна 180°.
Чтобы найти минимальный суммарный угол поворота робота, нужно исключить наибольший угол поворота. Этот угол будет смежным для наименьшего угла треугольника, который равен 30°.
Останется вычислить суммарный угол поворота робота:
(180°- 60°) + (180°- 90°) = 120° + 90° = 210°.
Таким образом, робототехника помогает ученикам разобраться в градусных величинах углов на примере движения робота-чертёжника. На занятиях, сконструировав такого робота, ученики могут потренироваться в определении значений углов, записав программы для изображения роботом различных геометрических фигур (квадрата, прямоугольника, ромба, трапеции). Это позволит ученикам наглядно и с интересом разобраться в данной теме геометрии.
При анализе заданий теоретического тура школьного этапа ВОШ за последние несколько лет, была составлена таблица (см. таблицу 2) с теми темами геометрии, которые использовались при решении [5]:
Таблица 2. Темы геометрии в ВОШ по робототехнике разных лет
| Год | Темы геометрии |
|---|---|
| 2020-2021 | Прямоугольник. Периметр и площадь прямоугольника. Соотношение между сторонами и углами прямоугольного треугольника. Тангенс угла наклона. Угол. Измерение углов. Смежные углы. Окружность. Радиус и диаметр окружности. Длина окружности. |
| 2019-2020 | Куб. Окружность. |
| 2018-2019 | Угол. Измерение углов. Окружность. |
| 2018-2017 | Геометрические фигуры в пространстве. Многоугольники. Прямоугольный треугольник. |
На основе данной таблицы можно сделать вывод, что в 2020-2021 резко увеличилось количество заданий по образовательной робототехнике, непосредственно связанных с геометрией. Это лишь подчеркивает значимость данного школьного предмета и его тесную взаимосвязь с робототехникой. Основной проблемой при освоении геометрии в школе остается недостаток наглядности при изучении некоторых тем, отсутствие практической составляющей. И именно робототехника помогает частично исправить сложившуюся ситуацию. Посредством конструирования и программирования роботов, ученики могут с интересом разобраться в проблемных для них темах геометрии, расширить свои познания в данной области. И наоборот, знания по геометрии помогут углубить познания учеников в робототехнике, что позволит решать задания творческого, повышенного уровня сложности, принимать участие в различных робототехнических олимпиадах и побеждать.
Organization at the classes on robotics of interdiscussion relations with geometry
Rubis E.A.,
undergraduate of 2 course of the Moscow City University, Moscow
Research supervisor:
Abushkin Dmitry Borisovich,
Associate Professor, Department of Informatics, Management and Technology, Institute of Digital Education of the Moscow City University, Ph.D.
Annotation. This article discusses the implementation of interdisciplinary connections with geometry in robotics classes. Some tasks of the school stage of the All-Russian Olympiad for schoolchildren in robotics for grades 7-8 are analyzed. It shows how preparation for these types of tasks can be carried out in robotics lessons.
Keywords: robotics, geometry, interdisciplinary communication, Olympiad.
- Григорьев С.Г., Курносенко М.В. Магистратура «Мехатроника, робототехника и электроника в образовании» как подготовка педагогов предметной области «Математика и информатика» // Информатика и образование. 2016. № 10. С. 53-55.
- Клокотов И.Ю. Развитие автоматизации и робототехники в современном мире // Международный журнал прикладных наук и технологий «Integral». 2019. № 3. С. 39.
- Поляничко К.С. Положение образовательной робототехники в системе современного образования России // Международный журнал гуманитарных и естественных наук. 2019. № 7-2. С. 40-42.
- Притыкин Ф.Н., Кайгородцева Н.В., Одинец М.Н., Крысова И.В. Робототехника как мотивация учения геометрии и графике // Ученые Омска – Региону. Материалы I Региональной научно-технической конференции. 2016. С. 92-100.
- Этапы Всероссийской олимпиады школьников в г. Москве // МНЦНО. 2020. .
- Grigoriev S.G., Kurnosenko M.V. Master's program «Mechatronics, Robotics and Electronics in Education» as the training of teachers in the subject area «Mathematics and Informatics» // Informatics and Education. 2016. № 10. Page: 53-55.
- Klokotov I.Yu. The development of automation and robotics in the modern world // International Journal of Applied Sciences and Technologies «Integral». 2019. № 3. Page: 39.
- Polyanichko K.S. The position of educational robotics in the system of modern education in Russia // International Journal of Humanities and Natural Sciences. 2019. № 7-2. Page: 40-42.
- Pritykin FN, Kaigorodtseva NV, Odinets MN, Krysova IV. Robotics as a motivation for teaching geometry and graphics // Scientists of Omsk - Region. Materials of the I Regional Scientific and Technical Conference. 2016. Page. 92-100.
- Stages of the All-Russian Olympiad for schoolchildren in Moscow // MNTSNO. 2020. (date of the address: 01.04.2021).
