Аннотация. В данной статье автором собраны и проанализированы документы, касающиеся одного из важных разделов истории математики, а именно: истории вычисления объёмов пирамид и конусов.
Ключевые слова: объём прямоугольной пирамиды, объём треугольной пирамиды, Архимед, Досифей, Евдокс, Демокрит.
Чтобы уверенно ответить на вопрос, кто раньше вычислил объём пирамиды: греки или египтяне, надо располагать достоверными документами, а именно: сохранившимися с древних времён артефактами. За тысячи лет многие ценнейшие артефакты исчезли и приходится восстанавливать историю математики буквально по крупицам. Тем ценнее те документы, которые дошли до нас.
Наиболее изученным из древнейших документов по математике можно считать математический папирус Ринда, датируемый II тысячелетием до н.э. Он полностью отреставрирован, расшифрован и издан для ознакомления максимально широкого круга заинтересованных читателей и исследователей.
Немалое значение для изучения начального периода развития математики имеет и Московский математический папирус Голенищева, относящийся по времени примерно к этому же периоду.
Что же касается более позднего периода (V в. до н.э. – III в. до н.э.), к которому относятся работы знаменитых греческих логиков и математиков: Демокрита, Евдокса Книдского, Евклида и Архимеда, то можно, к сожалению, констатировать полное отсутствие достоверных артефактов. Труды этих великих греческих математиков начали издаваться в Европе лишь в XIII – XVII веках н.э. Причём сведения о трудах греческих математиков зачастую черпались из оставшихся поныне неизвестными источников и арабских списков, которые, к слову сказать, так же, как и предшествовавшие им греческие рукописи, отсутствуют в открытом доступе. Поэтому авторство многих трудов по математике приходится принимать на веру, так же, как и достоверность информации о самих математиках.
В данной статье будет подробно исследован вопрос о том, кому принадлежит честь считаться первым в области вычисления объёмов пирамид и конусов.
Из письма, приписываемого Архимеду в предисловии к первой книге сочинения «О шаре и цилиндре», можно сделать вывод, что Евдокс Книдский впервые установил (и доказал), что объём пирамиды равен одной трети площади её основания, умноженной на высоту: V=1/3*S*h.
Чтобы убедиться в точности приписываемого Архимеду утверждения, взглянем на перевод соответствующего греческого отрывка (см. рисунок 1) [6], сделанный Петрушевским в книге «О шаре и цилиндре» 1825 года (см. рисунок 2).

Рис. 1. Греческий текст письма Архимеда Досифею

Рис. 2. Перевод письма Архимеда Досифею, сделанный Петрушевским
Первое, на что хочется обратить внимание - на то, что перевод Петрушевского сделан не везде корректно. Для сравнения, автор статьи предлагает свой вариант перевода греческого оригинала:
О шаре и цилиндре.
Архимед Досифея рад приветствовать!
Прежде разумеется отослал я тебе нами (мною) рассмотренные письма с доказательством... После же доставшихся нам (мне) теорем, достойных упоминания, мы занимались (я занимался) доказательствами своих. Вот же они: во-первых, что всякого шара поверхность в четыре раза больше есть, чем у наибольшего круга из тех, что в нём (в шаре); затем, что у всякого сегмента шара поверхность (её площадь) равна кругу, у которого радиус есть прямая от вершины сегмента, ведущая к краю круга, который является основанием сегмента; к тому же, что у всякого шара цилиндр, имеющий основание, равное наибольшему кругу из тех, что в шаре, и высоту равную диаметру шара, он (цилиндр) и в полтора раза больше шара (по объёму) и поверхность его (цилиндра) равна поверхности шара. Эти же самые случаи (исследований), по сути были уже раньше в области высказанных положений, непознанные же до меня в области геометрии теми, кто не обращали на них (на исследования) внимания и ничего своего (авторского) не придумали; поскольку у этих положений (формул) есть соразмерность (геометрическое согласие), то я не побоялся бы сравнивать свои (формулы) не только с другими геометрами рассмотренными теоремами, но и с решившими превзойти в области объёмов рассмотренные Евдоксом теоремы, что всякая пирамида есть одна треть призмы, имеющей основание то же самое, что у пирамиды, и высоту такую же (равную) и что всякий конус есть одна треть цилиндра, основание имеющего то же самое, что у конуса, и высоту такую же (равную), и конечно (превзойти) многих предшественников естественно в области положений (формул), до Евдокса рождённых, достойных упоминания геометров, что уходили, всеми будучи неузнанными и ранее будучи незамеченными.
Данный уже в советский период перевод отрывка из первой книги сочинений Архимеда «О шаре и цилиндре» также указывает на авторство Евдокса в области вычисления объёма пирамиды (см. рисунок 3) [5].

Рис. 3. Перевод отрывка из письма Архимеда Досифею, сделанный Мордухай-Болтовским
Можно согласиться с утверждением Архимеда, что до Евдокса греческим математикам была неизвестна теорема о вычислении объёма пирамиды. В отношении греческих геометров, возможно, это утверждение истинно, но не в отношении египетских геометров. В последней фразе приведённого отрывка из послания Архимеда содержится упоминание о многих «до Евдокса рождённых, достойных упоминания геометров» (см. перевод автора статьи). Естественно предположить, что имеются в виду египетские математики, математические достижения которых перенимали впоследствии греческие математики, в том числе и Архимед.
Это предположение подтверждается ценнейшим египетским артефактом, хранящимся в Пушкинском музее. А именно: в задаче №14 Московского математического папируса Голенищева, относящегося ко II тысячелетию до н.э., приводятся расчёты объёма не просто пирамиды, а усечённой пирамиды, что убедительно доказывает высочайший уровень развития в этой области египетской математики [3].
Как же быть с Евдоксом Книдским? Действительно ли он первым доказал справедливость формулы вычисления объёма пирамиды?
В египетских артефактах, дошедших до нас, нет задач по расчёту объёмов треугольных пирамид, доказательством формулы для расчёта объёма которых и занимался Евдокс Книдский. Поэтому расчёт объёма треугольной пирамиды возможно и был впервые проведён Евдоксом Книдским.
Для своего доказательства Евдокс Книдский использовал знание объёма треугольной призмы, а также доказательство того, что объём треугольной призмы складывается из трёх равных по объёму треугольных пирамид. Причём, равенство объёмов этих треугольных пирамид следует из доказательства того, что пирамиды, имеющие равные высоты и равные площади основания, имеют равный объём. Для доказательства последнего Евдокс Книдский прибегал к мысленному рассечению пирамиды на множество тонких слоёв, из которых складывался общий объём пирамиды (см. рисунок 4).
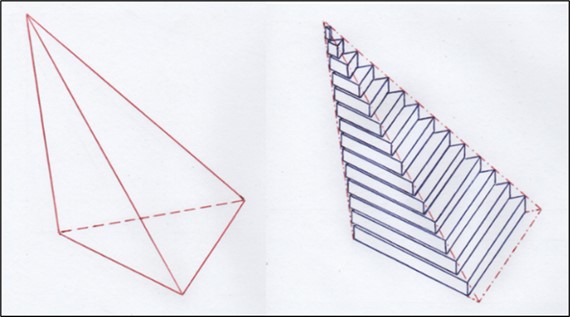
Рис. 4. Метод рассечения пирамиды на тончайшие слои
Вероятно, метод рассечения пирамиды на тончайшие слои был предложен Демокритом. Отсюда, возможно, и возникло неверное мнение, что Демокрит первым стал вычислять объём пирамиды.
Но ведь треугольную пирамиду можно представить, как состоящую из множества малых прямоугольных пирамид (см. рисунок 5).
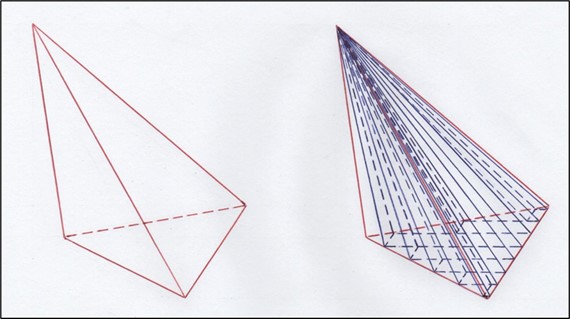
Рис. 5. Метод рассечения треугольной пирамиды на малые прямоугольные пирамиды
То, что египтяне умели вычислять объём прямоугольной пирамиды и, безусловно, знали доказательство этого вычисления [3], как минимум, ставит под сомнение приоритет в этой области Евдокса Книдского. Более того, пирамида с любым многоугольным основанием может быть представлена не только, как состоящая из n-ного количества треугольных пирамид, но и разбита на сколь угодно большое количество малых прямоугольных пирамид. В любом случае, объём будет вычислен по одной и той же формуле: V=1/3*S*h.
Что же касается вопроса: «А какую пирамиду считать элементарной: прямоугольную или треугольную?», то ответ лежит в истоках геометрии. Вспомним, как вычислялась площадь треугольника, как состоящего из двух прямоугольных треугольников, а площади прямоугольных треугольников, в свою очередь, вычислялись, как половины площадей соответствующих прямоугольников. Более того, измерение площадей на практике всегда проще, когда эти площади прямоугольные. Поэтому, по мнению автора статьи, элементарной пирамидой следует считать именно прямоугольную пирамиду, а не треугольную.
В заключении, автор статьи готова представить вычисление объёма треугольной пирамиды, используя египетский метод вычисления объёма пирамиды. Он аналогичен египетскому методу вычисления объёма прямоугольной пирамиды.
Нам потребуется лемма об объёмах подобных треугольных пирамид, вписанных в подобные прямоугольные параллелепипеды. Причём, одно из рёбер пирамиды совпадает с её высотой (см. рисунок 6).
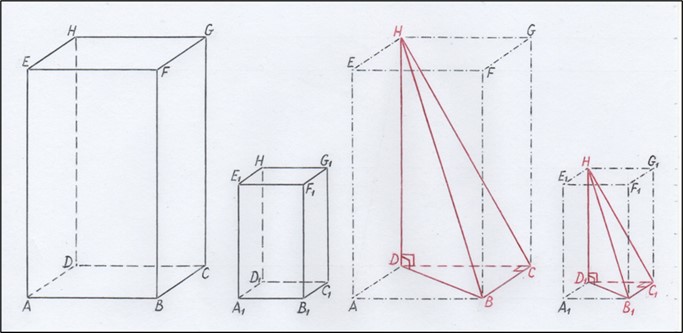
Рис. 6. Подобные параллелепипеды и вписанные в них подобные треугольные пирамиды
Легко доказать [3], что объёмы вписанных треугольных пирамид относятся друг к другу, как объёмы соответствующих прямоугольных параллелепипедов.
Далее проведём рассечение данной треугольной пирамиды тремя плоскостями: первая проходит параллельно основанию через середину её высоты, а две других плоскости рассекают пирамиду перпендикулярно плоскости её основания, как показано на рисунке 7.
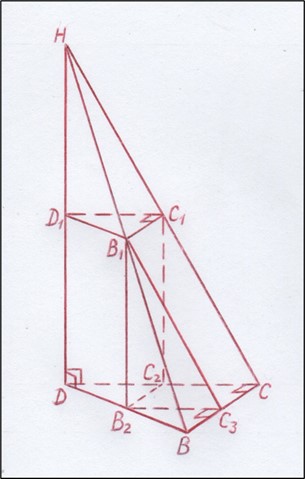
Рис. 7. Рассечение треугольной пирамиды тремя плоскостями
В результате пирамида оказывается рассечённой на 4 фигуры: прямую треугольную призму, половину прямоугольного параллелепипеда, а также две равных треугольных пирамиды, объём каждой из которых равен 1/8 исходной треугольной пирамиды.
 |
 |
Рис. 8. Модель рассечённой пирамиды с рисунка 7
Составим уравнение для объёма исходной треугольной пирамиды, учитывая, что её объём складывается из объёмов прямой треугольной призмы, имеющей в основании прямоугольный треугольник, половины прямоугольного параллелепипеда и двух равных треугольных пирамидок, каждая из которых имеет объём в 8 раз меньший, чем у исходной пирамиды. После несложных вычислений получаем: V=1/3*S*h, где S – площадь треугольного основания пирамиды, а h – высота пирамиды.
Мы получили формулу для вычисления объёма треугольной пирамиды, у которой боковое ребро совпадает с её высотой, а в основании лежит прямоугольный треугольник. Добавляя к ней другую соответствующую пирамиду, у которой боковое ребро совпадает с высотой, а в основании также лежит прямоугольный треугольник, мы получаем пирамиду, у которой, хотя ребро и совпадает с её высотой, но в основании такой пирамиды уже лежит произвольный треугольник DBM (см. рисунок 9).
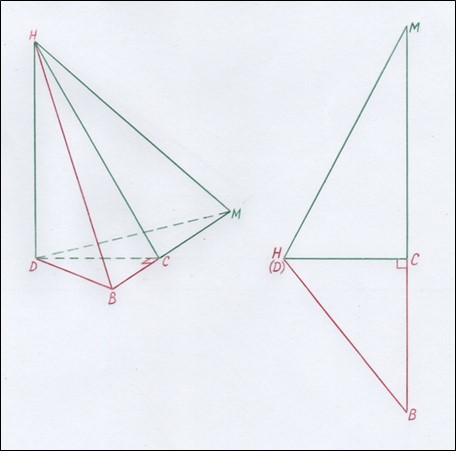
Рис. 9. Треугольная пирамида, у которой боковое ребро совпадает с её высотой, а в основании лежит произвольный треугольник DBM (справа вид этой пирамиды сверху)

Рис. 10. Модель пирамиды с рисунка 9
В основании треугольной пирамиды могут быть любые треугольники, являющиеся композицией из двух прямоугольных треугольников (см. примеры на рисунке 11).
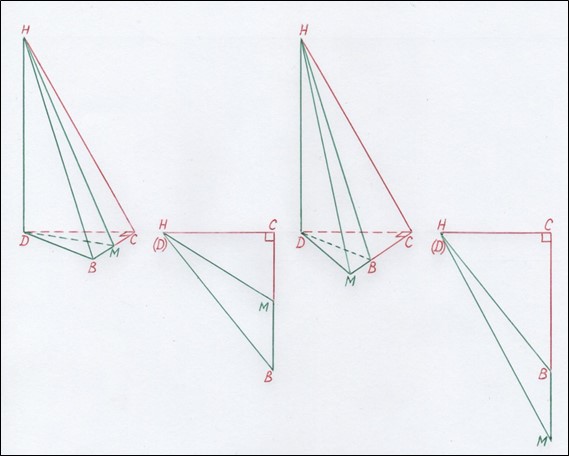
Рис. 11. Треугольник DBM в основании пирамиды, как композиция из прямоугольных треугольников DBC и DMC
При этом, объём пирамиды также вычисляется по формуле: V=1/3*S*h.
Не трудно показать, что любая треугольная пирамида может быть представлена, как композиция из нескольких треугольных пирамид, имеющих общее боковое ребро, совпадающее с их высотой (см. рис. 12).
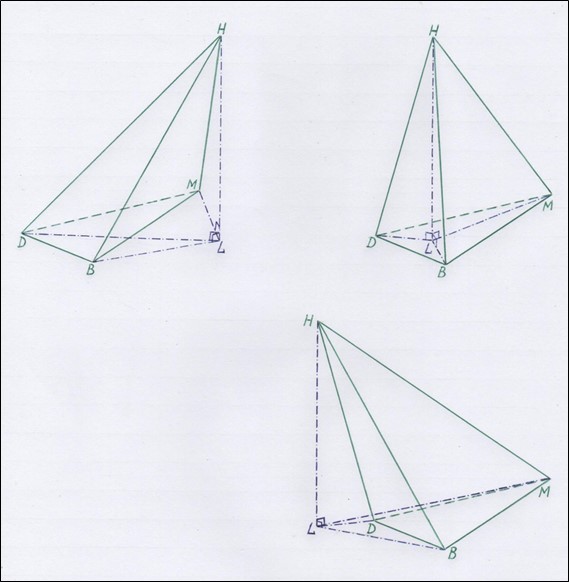
Рис. 12. Пирамида DBMH, как композиция из трёх пирамид: DBLH, DLMH и BLMH
На рисунке 12 мы видим, что пирамида DBMH в первом случае представлена, как сложение двух пирамид DBLH и DLMH за вычетом пирамиды BLMH. Во втором случае пирамида DBMH сложена из трёх пирамид: DBLH, DLMH и BLMH. И наконец, в последнем случае пирамида DBMH образована из пирамиды BLMH, из которой вычитаются пирамиды DBLH и DLMH.
Таким образом, мы показали, что формула для объёма пирамиды V=1/3*S*h будет верна для любой треугольной пирамиды.
Поэтому можно утверждать, что вряд ли для египтян было недоступно вычисление объёма треугольной пирамиды.
Ну и в качестве последнего аргумента, свидетельствующего в пользу египетских геометров в вопросе вычисления объёма пирамид (да и конусов), может убедительно служить то, что и Демокрит, и Евдокс Книдский, и Евклид, объединивший достижения древнегреческих математиков в своём математическом труде «Начала», проходили обучение по математике в Египте.
Список литературы:
- Вейсман А.Д. Греческо-русский словарь. М.: Греко-латинский кабинет Ю.А. Шичалина, 1991. 1371 с.
- Соболевский С.И. Древнегреческий язык: Учебник. Репринтное издание. Серия «Классика». М.: Лист Нью, 2003 г. 617 с.
- Костюк В.Я. Как древние египтяне вычисляли объём пирамиды без интегрирования // «Наука в Мегаполисе. Science in a Megapolis», 2025. №13(81). (дата обращения: 12.12.2025).
- Архимедъ. Двѣ книги о шарѣ и цилиндрѣ, измѣренiе круга и леммы. Переводъ съ Греческаго (Леммы съ Латинскаго) Ө.Петрушевскаго. Санктпетербургъ: Типографiя Департамента Народнаго Просвѣщенiя, 1825. 239 с. / Творения Архимеда. Две книги о шаре и цилиндре, измерение круга и леммы / пер. с греч. (леммы с лат.) О. Петрушевского, цензор А. Бируков. Санкт-Петербург: Типография Департамента народного просвещения, 1825. 239 с. (дата обращения: 11.12.2025).
- Евклид. Начала (перевод Д.Д. Мордухай-Болтовского). Кн. 11-15. Москва-Ленинград: Государственное издательство технико-теоретической литературы, 1950. 330 с. (дата обращения: 13.12.2025).
- Archimedes, Oeuvres Archimedes. T. 1: De la sphère et du cylindre; La mesure du cercle; Sur les conoïdes et les sphéroïdes / Archimède; Texte établi et trad. par Charles Mugler. Paris: Les belles Lettres, 1970. 258 p. (дата обращения: 12.12.2025).
Who was the first to calculate the volume of the pyramid: the Greeks or the Egyptians?
Kostyuk V.Y.,
student of 3 course of the Moscow City University, Moscow
Abstract. In this article, the author has collected and analyzed documents related to one of the important sections of the history of mathematics, namely: the history of calculating the volumes of pyramids and cones.
Keywords: the volume of a right pyramid, the volume of a triangular pyramid, Archimedes, Dositheus, Eudoxus, Democritus.
References:
- Veisman A.D. Greek-Russian dictionary. Moscow: The Greek-Latin cabinet of U.A. Shichalin, 1991. 1371 p.
- Sobolevsky S.I. Ancient Greek language: Textbook. Reprint edition. The «Classics» series. Moscow: Liszt New, 2003 617 p.
- Kostyuk V.Y. How the ancient Egyptians calculated the volume of a pyramid without integral calculus // Science in a Megalopolis, 2025. №13(81). (date of the address: 12.12.2025).
- Архимедъ.Two books about the sphere and the cylinder, the circle theory and lemmas. Translation from Greek (Lemmas from Latin) O.Petrushevsky. St. Petersburg: Printing House of the Department of National Education, 1825. 239 p. (date of the address: 11.12.2025).
- The Elements. Books 11-15 / translated from Greek by D.D. Mordukhai-Boltovskoy. Moscow-Leningrad: State Publishing House of Technical and Theoretical Literature, 1950. 330 p. (date of the address: 13.12.2025).
- Archimedes, Archimedes Works. T. 1: Of the sphere and the cylinder; The measurement of the circle; On conoids and spheroids / Archimedes; Text established and translated by Charles Mugler. Paris: The Beautiful Letters, 258 p. (date of the address: 12.12.2025).
