Аннотация. Статья посвящена проблемам изучения Московского математического папируса Голенищева, а также продолжает начатую великим русским египтологом Б.А. Тураевым работу по расшифровке задач, изложенных в этом папирусе. В заключении статьи впервые приводится полная расшифровка задачи №4, которая сохранилась в папирусе Голенищева лишь фрагментарно.
Ключевые слова: Московский математический папирус Голенищева, Б.А. Тураев, В.В. Струве, задача №14, задача №4.
Одним из наиболее известных египетских артефактов, привезённых в Россию, является знаменитый математический папирус Голенищева, или Московский математический папирус.
Википедия сообщает, что «ныне «папирус Голенищева» находится в Музее изобразительных искусств им. А.С. Пушкина в Москве» [1]. Но это верно лишь отчасти, причём в прямом смысле. В Пушкинском музее выставлен для посетителей в открытом доступе лишь крошечный фрагмент этого поистине значительного артефакта. А именно, из 25 задач, записанных на этом папирусе, в музее можно увидеть лишь часть 13-й задачи и 14-ю задачу (см. рисунок 1-2).

Рис. 1. Окончание 13-й задачи и начало 14-й задачи из папируса Голенищева

Рис. 2. 14-я задача из папируса Голенищева
Видимо поэтому, когда ищешь информацию о задачах Московского математического папируса, то неизменно натыкаешься именно на 14-ю задачу. Причём в открытом доступе практически невозможно увидеть её в разборчивой оригинальной иератической записи, и приходится довольствоваться лишь общим описанием, сделанным на основе публикации В.В. Струве, которую он разместил в 1930 году в немецком журнале «Quellen und Studien zur Geschichte der Mathematik» на немецком же языке [5]. Не правда ли, странно выглядит, что один из известнейших основоположников отечественной египтологии не удосужился опубликовать статью о столь важном артефакте в своей стране на русском языке? Более того, за почти столетний период, прошедший со времени этой публикации, у нас в стране не только не был опубликован перевод этой статьи на русский язык, но даже доступ к немецкой публикации практически невозможен. Но не будем углубляться в причины этого. Так же, как и не будем искать причину, почему в «Хрестоматии по истории древнего мира» под редакцией В.В. Струве отсутствовал полноценный перевод Мемфисского декрета [3].
Но уж если мы упомянули столь знаменитого «отечественного» египтолога, то мы просто обязаны отдать должное истинному основателю отечественной египтологии - Борису Александровичу Тураеву. Задолго до оригинальной публикации Струве в немецком журнале, изданном в 1930 году, Тураев исследовал загадочный математический папирус Голенищева и впервые проложил путь к расшифровке описанных там задач. Причём сообщения о своих достижениях он делал на русском языке. И на русском же языке в «Известиях Российской академии наук» в 1925 году вышла статья Д.П. Цинзерлинга с описанием достижений Б.А. Тураева, в том числе и по расшифровке Московского математического папируса [4]. Информация о расшифровке самых интересных пяти задач из этого папируса была представлена Тураевым на Заседании Отделения Исторических Наук и Филологии 16 апреля 1919 года, что значительно раньше выхода немецкой статьи В.В. Струве [2]. Более того, изменения, внесённые в расшифровку этих задач В.В. Струве и его помощником Ю.Я. Перепёлкиным, явно ошибочны, о чём в частности свидетельствует отзыв о публикации В.В. Струве английского египтолога Эрика Пита, который не согласен со Струве во многих вопросах: «In the remarks which follow I venture to disagree with Struve upon many points…» [6].
Исходя из вышсказанного, важно изучать труды выдающегося отечественного египтолога Б.А. Тураева, к сожалению, уже почти забытые. Приводим текст пяти полностью расшифрованных Тураевым задач из Московского математического папируса (см. рисунки 3-7). Сразу надо отметить, что нумерация задач из математического папируса Голенищева у Тураева начинается с задачи №6. Объяснить это можно тем, что первые задачи имеют очень плохую степень сохранности, и Тураев даже не пытался их расшифровывать.

Рис. 3. Задача №6 из папируса Голенищева, расшифрованная Б.А. Тураевым

Рис. 4. Задача №7 из папируса Голенищева, расшифрованная Б.А. Тураевым
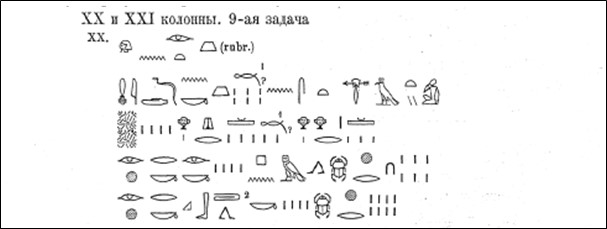

Рис. 5. Задача №14 из папируса Голенищева, расшифрованная Б.А. Тураевым


Рис. 6. Задача №17 из папируса Голенищева, расшифрованная Б.А. Тураевым


Рис. 7. Задача №21 из папируса Голенищева, расшифрованная Б.А. Тураевым
Не все задачи папируса Голенищева были полностью расшифрованы Тураевым. Струве также не дал полной расшифровки задач из Московского математического папируса.
Автор этой статьи, продолжая научный труд Тураева, жизнь которого оборвалась в 1920 году, провела работу по полному восстановлению и расшифровке текста задачи №4 из Московского математического папируса. Она входит в число первых пяти задач, которые Тураев даже не пытался расшифровать из-за их плохой сохранности. А Струве привёл лишь скудные сохранившиеся фрагменты из этих задач. Фрагменты задачи №4 без перевода и каких-либо существенных комментариев были приведены в статье «Московский Математический папирус» в Wikisource (см. рисунок 8) [7].
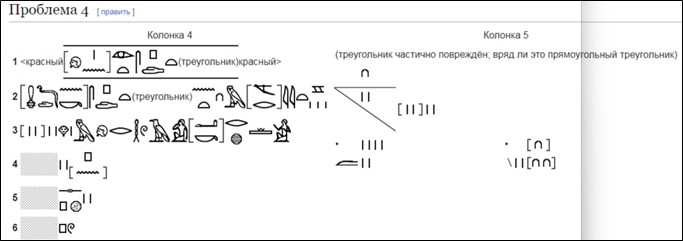
Рис. 8. Немногие сохранившиеся фрагменты задачи №4 из папируса Голенищева
Как видно из приведённой выше иллюстрации, более половины текста задачи №4 утрачено. Тем не менее, анализируя эти немногие сохранившиеся фрагменты задачи №4, автор статьи сумела не только восстановить смысл задачи, но и, основываясь на работах Тураева, полностью восстановила иероглифическое написание утраченных фрагментов задачи №4.
Далее предлагаем читателям ознакомиться с полностью восстановленным иероглифическим текстом задачи №4 (см. рисунок 9), а также его переводом на русский язык.

Рис. 9. Иероглифический текст задачи №4 из папируса Голенищева, восстановленный автором статьи В.Я. Костюк
Перевод иероглифического текста задачи №4, также выполненный автором статьи, гласит:
«Задача о прямоугольном треугольнике.
Подобный названному тебе прямоугольный треугольник, у которого 10 – это боковая сторона,
4 – это основание фигуры. Даю тебе порядок расчёта
площади её (фигуры). Сделай 1/2 от 4. Это 2 есть.
Сделай умножение 10 в 2 раза.
Площадь её (фигуры) это есть».
Далее в описании задачи приводятся попарно числа: 1 – 4; 1/2 – 2
Эти числа относятся к 4-й строке задачи («Сделай 1/2 от 4. Это 2 есть»).
Кроме того, другие числа, также приведённые попарно: 1 – 10; 2 – 20, относятся к 5 строке задачи («Сделай умножение 10 в 2 раза»). Причём важно заметить, что последняя пара чисел (2 – 20) сопровождается характерным штрихом (\), что указывает на окончательный этап вычисления, в результате которого мы получили ответ – 20.
Разумеется, что работа по расшифровке Московского математического папируса должна быть продолжена с целью расшифровки и доведения до массового читателя как можно более полного содержания папируса Голенищева. Поэтому, пользуясь медиаплатформой данного журнала, призываю хранителей этого папируса провести оцифровку этого важного документа и открыть доступ к ней для заинтересованных исследователей и читателей.
Список литературы:
- Московский математический папирус. Википедия. (дата обращения: 28.10.2025).
- Одинец В.П. О работах трёх математиков, выпускников Казанского и Петербургского университетов, погибших в Великой Отечественной войне // Вестник Сыктывкарского университета. Сер. 1: Математика, Механика. Информатика, 2024. Вып. 2(51). С. 57-72. (дата обращения: 28.10.2025).
- Струве В.В. Хрестоматия по истории древнего мира. М.: Упедгиз, 1951. 340 с.
- Цинзерлинг Д.П. Геометрия у древних египтян // Извѣстія Россiйской Академіи Наукъ. VI серiя, том 19, выпуск 12, 1925. С. 541-568. (дата обращения: 02.11.2025).
- Struve W.W., Turajeff B.A. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau // Quellen und Studien zur Geschichte der Mathematik. Abt. A. Quellen. Berlin: Julius Springer, 1930. XII, 197 p.
- Reviewed Work:Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau by W.W. Struve, Review by: T. Eric Peet // The Journal of Egyptian Archaeology – Published By: Sage Publications, , 1931. Vol. 17, №1/2.: 154-160.
- Moscow Mathematical Papyrus. Wikisource. (дата обращения: 05.11.2025)
About the Golenishchev Papyrus and Problems №14 and №4
Kostyuk V.Y.,
student of 3 course of the Moscow City University, Moscow
Abstract. The article is devoted to the problems of studying the Golenishchev Moscow Mathematical Papyrus, and also continues the work begun by the great Russian Egyptologist B.A. Turaev on deciphering the problems described in this papyrus. At the end of the article a complete transcription of problem №4, which has been preserved in the Golenishchev papyrus only in fragments, is provided for the first time.
Keywords: Golenishchev's Moscow Mathematical Papyrus, B.A. Turaev, V.V. Struve, Problem №14, problem №4.
References:
- Moscow Mathematical Papyrus. Wikipedia. URL: (date of the address: 28.10.2025).
- Odinets V.P. On the works of three mathematicians, graduates of Kazan and St. Petersburg Universities, who died in the Great Patriotic War // Bulletin of Syktyvkar University. Ser.1: Mathematics, Mechanics. Computer science, 2024 Ed. 2(51).: 57-72. (date of the address: 28.10.2025).
- Struve V.V. Anthology on the history of the ancient world. Moscow:Upedgiz,1951. 340 р.
- Zinzerling D.P. Geometry of the ancient Egyptians // Proceedings of the Russian Academy of Sciences. VI Series, Vol. 19, Edition 12, 1925.: 541-568. (date of the address: 02.11.2025).
- Struve W.W., Turajeff B.A. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau // Quellen und Studien zur Geschichte der Mathematik. Abt. A. Quellen. Berlin: Julius Springer, 1930. XII, 197 p.
- Reviewed Work:Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau by W.W. Struve, Review by: T. Eric Peet // The Journal of Egyptian Archaeology – Published By: Sage Publications, Ltd., 1931. Vol. 17, №1/2.: 154-160.
- Moscow Mathematical Papyrus. Wikisource. (date of the address: 05.11.2025).
