Выпуск: №11(56) Исследования молодых ученых

Раздел: Психолого-педагогические науки

Опубликовано: 30 декабря 2023

Код уникальной десятичной классификации: 372.851

Автор: Гуськова Анна Алексеевна

студент 3 курса ГАОУ ВО МГПУ, г. Москва

Научный руководитель: Некрашевич Ольга Александровна

преподаватель департамента педагогики и методики начального общего образования Института среднего профессионального образования им. К.Д. Ушинского ГАОУ ВО МГПУ

Аннотация. Статья посвящена проблеме формирования познавательного интереса к устным вычислениям у младших школьников на уроках математики. Рассмотрены виды математических разминок. Разработана собственная система организации математической разминки в первом классе.

Ключевые слова: устные вычисления, математическая разминка.

Освоение приемов устных вычислений является одной из главных задач обучения математике, так как именно на их основе строится формирование вычислительных навыков, умение решать примеры, задачи и уравнения. Устные вычисления для младших школьников имеют большое значение. Ученики должны не только сознательно усвоить приёмы вычислений, но и приобрести твёрдые вычислительные навыки, которые формируются только постоянными тренировками.

Процесс овладения вычислительными навыками сложен. Сначала обучающиеся усваивают вычислительные приемы, а затем в результате тренировок учатся достаточно быстро выполнять вычисления, а в табличных случаях запоминают результаты наизусть [2].

Проблема формирования у учащихся вычислительных умений и навыков всегда привлекала особое внимание психологов, методистов, учителей. В методике преподавания математики этим занимались такие деятели, как: Е.С. Дубинчук, А.А. Столяр, С.С. Минаева, Н.Л. Стефанова, Я.Ф. Чекмарева, М.А. Бантова, М.И. Моро, Н.Б. Истомина, С.Е. Царева и др. Каждое из их исследований внесло определенный вклад в разработку и совершенствование той методической системы, которая используется в практике обучения и нашла отражение в учебниках математики [1].

Для развития у учащихся вычислительных навыков используют разные методы, формы и приёмы работы, например организация на каждом уроке математики этапа математической разминки. Именно в процессе математической разминки и происходит закрепление умения применять различные приёмы вычислений и формирование вычислительного навыка.

К сожалению, не все младшие школьники бывают включены в этот этап урока. Им он кажется скучным, неинтересным и трудным процесс вычислений в уме. Это может быть связано с некоторыми причинами.

1. Использование технических средств

В современном мире существует достаточно большое количество электронных вычислительных средств, таких как: смартфон, калькулятор и другие устройства. Они выполняют вычислительные действия за ребёнка, которому уже не нужно считать самостоятельно.

2. Отсутствие практики

В повседневной жизни дети могут не получать достаточной практики устных вычислений, что может привести к снижению интереса к этому виду деятельности.

3. Сложность устных вычислений

Устные вычисления требуют запоминания большого количества операций. Это может быть сложным для детей, которые только начинают изучать математику или она трудно им даётся.

Как сделать так, чтобы ученик сам захотел максимально включиться в процесс формирования своих вычислительных навыков, в многократные тренировки, которые происходят в процессе математической разминки на каждом уроке математики? Как сформировать познавательный интерес к этому виду деятельности?

Познавательный интерес – избирательная направленность личности на предметы и явления окружающей действительности. Эта направленность характеризуется постоянным стремлением к познанию, к новым, более полным и глубоким знаниям [3].

Не всегда «сухие примеры» устного счёта привлекательны для детей, а когда нет интереса, то нет и мотивации прикладывать усилия для освоения вычислительных приёмов. Формировать этот интерес необходимо начиная с первых уроков математики в начальной школе.

Во время прохождения производственной практики были проведены уроки математики в разных классах. Перед каждым занятием возникали вопросы – какие задания и в какой форме можно предложить обучающимся на уроках математики на этапе математической разминки для формирования у них познавательного интереса к устным вычислениям.

Были использованы разные виды математической разминки. Это математический диктант, математическая раскраска, интерактивные дидактические игры. Конечно же, когда проводятся уроки в разных школах и классах, единую систему организации математической разминки выстроить сложно, практически невозможно. Но, используя различные формы проведения математической разминки в своей практике, можно выделить те, которые наиболее интересны для школьников и целесообразны для реализации задачи закрепления устных вычислительных навыков. В результате возникло понимание, как можно вовлечь всех учащихся в работу на этом этапе урока, работая учителем начальных классов.

Подготовка и реализация на практике видов деятельности, направленных на формирование познавательного интереса к устным вычислениям у младших школьников на уроке математики посредством организации разных видов математической разминки, отражает переход на образовательные стандарты начального общего образования нового поколения [4, с. 9], стимулирует осознанное принятие профессиональной позиции в работе с обучающимися [5, с. 31]. Особое значение апробация самостоятельно разработанных материалов имеет для целенаправленно организованного процесса становления и развития профессиональной позиции субъектности [6, с. 37].

Но сначала необходимо остановиться на видах математической разминки, которые можно использовать на уроках. Они представлены ниже.

1. Математический диктант «Математическая узнавайка», по результатам выполнения которого дети знакомятся с интересным познавательным фактом. Его проведение можно организовать несколькими способами. Обучающимся диктуются примеры, которые они должны решить. Каждый ответ, который они получают, соответствует определённой букве. Сопоставляя числа с буквами у обучающихся получается слово. Об этом слове учитель рассказывает новую и интересную информацию. Возможен ещё один вариант проведения данного вида работы. Сначала учитель показывает картинку или фотографию и спрашивает, знают ли дети что это (или кто это). Для того, чтобы узнать, надо выполнить математический диктант и сопоставить получившийся ответ с буквой, которая ему соответствует.
2. Круговые примеры, которые для младших школьников можно представить в виде красочной карточки для самостоятельного выполнения, что повысит познавательную активность учеников, будет способствовать развитию логического мышления, укрепит навыки счета. Для младшего школьника такой вид заданий хорош тем, что получение неверного ответа не даст учащемуся перейти к следующему примеру, тем самым ребенок контролирует правильность своего решения.
3. Интерактивные упражнения, выполненные на разных платформах. Как правило они используются для фронтальной работы, но при наличии планшетов в классе можно их давать на парное или индивидуальное выполнение. Например, «Математический пазл». Обучающиеся сканируют QR-код, который является ссылкой на пазл, или игра выводится на интерактивную доску. На каждой детали пазла написан пример. Задача обучающегося его решить. Если пример будет решён верно, то деталь пазла перевернется. Собранная картинка пазла может стать проблемным вопросом, на который они найдут ответ в течение урока, мотивирующим словом и т.д. Сюрпризность итога этого упражнения повышает мотивацию учеников к его выполнению.
4. Групповые соревновательные вычисления, когда в команде учащиеся по очереди решают примеры на время. Например, «Математическая цепочка». Обучающиеся класса разделены на команды по рядам. Учитель даёт лист с примерами тому, кто сидит за первой партой, ребенок решает его, затем лист с его ответом на пример передаётся назад. Побеждает команда, правильно решившая все примеры быстрее всех. Групповые соревнования также направлены на развитие коммуникативных универсальных учебных действий, таких как сотрудничество с одноклассниками для достижения общей цели, ответственное выполнение своей части работы, несение ответственности за получившийся результат.
5. Математические фокусы, которые могут удивить детей, развить познавательный интерес к математике. В основе фокуса может лежать та или иная закономерность, которая основывается на свойствах арифметических действий и порядке их выполнения. Эти закономерности в начальном школьном курсе, как правило, не изучаются. Но педагог, демонстрирующий «фокус», ставит перед собой цель не обучить детей этим правилам, а через выполнение устных вычислений в занимательной форме пробудить интерес к познанию нового, необычного, воспитывать культуру исследовательской деятельности.
6. «Математический манджонг». Данную математическую разминку стоит давать для групповой (парной) работы. На карточках, которые лежат рядом друг с другом на столе, написаны примеры и ответы на них. Задача детей убирать эти карточки парами, то есть пример и ответ на него. Можно давать это задание на время, тем самым добавив соревновательный элемент в математическую разминку.
7. «Математический дартс». В середине игрового круга на слайде написан пример, а вокруг него ответы. (один верный, а 3 не правильных). Задача обучающихся посчитать пример и выбрать правильный ответ, указав на него лазерной указкой. (Указку даёт учитель самостоятельно ученику).

Организуя в течение недели каждый день математическую разминку в разной форме, учитель получит положительный результат в формировании познавательного интереса к устным вычислениям. У учеников возникнет интерес и желание заниматься таким видом деятельности, как устные вычисления. Кроме того, систематическое проведение разнообразных видов математической разминки поможет обучающимся расширить свой кругозор в области математики и не только. Так же разминка позволит учителю оценить уровень подготовки учеников, выявить проблемные моменты и предоставить помощь для их устранения.

На основе изученных видов математической разминки была составлена авторская система организации проведения математической разминки в 1 классе в 4 четверти по системе обучения «Школа России». Для каждой недели разработаны задания на каждый урок математики для проведения этого этапа в разной форме. Ниже представлены варианты математической разминки на одну неделю для четырёх уроков по темам, соответствующим календарно-тематическому планированию:

Тема 1: сложение однозначных чисел с переходом через десяток вида (…)+5.
Математическая разминка: «Математический дартс».
Цель: закрепление приёмов сложения однозначных чисел вида (…)+2, (…)+3, (…)+4, а также выполнения нумерационного сложения.
Задание: Перед вами мишени (см. рисунок 1), на которых написаны пример и четыре ответа на него. Среди этих ответов один верный, а остальные три нет. Решите пример и лазерной указкой укажите на его ответ.

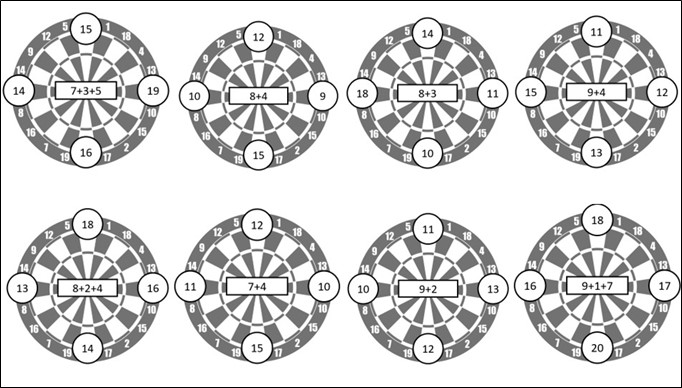
Рис.1 Математический дартс

Тема 2: сложение однозначных чисел с переходом через десяток вида (…)+6.
Математическая разминка: «Математическая узнавайка».
Цель: закрепить умение выполнять сложение и вычитание в пределах 10, нумерационное сложение в пределах 20 и табличное сложение однозначных чисел изученных случаев.
Задание: Учитель демонстрирует на доске фотографию трубкозуба (см. рисунок 2) и спрашивает учеников, знают ли они, как называется это животное.

Рис.2. Трубкозуб

Для того, чтобы узнать название, надо выполнить математический диктант. Учитель диктует примеры:

• девять плюс пять;
• первое слагаемое восемь, второе три, найдите сумму;
• из суммы чисел семь и три вычесть девять;
• к восьми прибавить два и прибавить девять;
• из десяти вычесть два;
• одиннадцать уменьшить на один, а затем увеличить на восемь;
• к семи прибавить пять;
• из восьми вычесть пять и ещё два;
• из девяти вычесть ноль и прибавить один.

После проверки по эталону на доске демонстрируется таблица.

Каждому ответу на пример соответствует своя буква. Напишите рядом с ответами соответствующую букву. У детей получается слово: трубкозуб.

Далее учитель сообщает небольшую познавательную информацию об этом животном: «Самым необычным животным на земле можно смело назвать трубкозуба. Он не похож ни на одно известное нам животное. Его происхождение до сих пор остается загадкой. Конечности трубкозуба напоминают копытца, тело – кенгуру, мордочка – муравьеда с заячьими ушами и свиным пятачком. Животное обитает в Африке. Это безобидное животное, живущее в норах. Они отличные землекопы. Питается трубкозуб муравьями, личинками жуков и саранчи, за сутки может съесть более 50 тысяч насекомых».

Тема 3: сложение однозначных чисел с переходом через десяток вида (…)+7.
Математическая разминка: «Математическая цепочка».
Цель: закрепить умение выполнять сложение и вычитание в пределах 10, нумерационное сложение и вычитание в пределах 20 и табличное сложение однозначных чисел изученных случаев.
Задание: Сейчас мы будем решать примеры в командах. Каждый ряд – это одна команда. Вам будут диктовать примеры, а вы по очереди будете решать. То есть первый и второй примеры решают те, кто сидит за первой партой, пишут ответ на маркерной доске и передают её дальше, следующие решают другие примеры и так же записывают только ответ. Победит та команда, которая правильно решит все примеры. Те учащиеся, кто не пишет в данный момент на доске, молча находят ответ, он нам пригодится при проверке.

Примеры:

• из 10 вычесть 6,
• к получившемуся числу прибавить 5,
• прибавить еще 5,
• вычесть 4,
• из получившегося числа вычесть ещё 2,
• прибавить 6,
• уменьшить на 10,
• увеличить на это же число,
• вычесть ещё 5,
• увеличить получившееся число на 7.

Тема 4: сложение однозначных чисел с переходом через десяток вида (…)+8, (…)+9.
Математическая разминка: «Математический пазл».
Цель: закрепить умение выполнять сложение однозначных чисел с переходом через десяток изученных видов.
Выполняется или фронтально на интерактивной доске, или на планшете, если есть необходимое оборудование в классе.
Задание: Решите примеры, перейдя по ссылке (см. рисунок 3):

Рис 3. QR – код задания «Математический пазл»

Мы видим, что на протяжении недели каждый день организуется математическая разминка разного вида. Для младшего школьника, особенно для ученика первого класса всегда интересен эффект неожиданности. Занимательная и познавательная форма проведения устного счёта положительно отражается на мотивации детей выполнять тренировочные упражнения для формирования вычислительного навыка.

Таким образом, организация разных видов математических разминок способствует развитию познавательного интереса к устным вычислениям у младших школьников на уроке математики.

Литература:

1. Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах. М.: Просвещение, 2004. 335 с.
2. Гаврилина О.В. Принцип индивидуального подхода в процессе формирования вычислительных навыков у младших школьников // Вестник Белгородского института развития образования. 2018. 139 с.
3. Трегубова Н.Е. Активизация познавательной деятельности младших школьников на уроках математики // Молодой ученый. 2014. №18(77). С. 652-655.
4. Чозгиян О.П. Переход на образовательные стандарты начального общего образования нового поколения: актуальные проблемы обновления подходов к образованию на дошкольной ступени // Дошкольник. Методика и практика воспитания и обучения. 2023. №1. С. 3-9.
5. Чозгиян О.П. Развитие осознанности принятия профессиональной позиции у будущих учителей (уровень – СПО) // Большая конференция МГПУ: сборник тезисов. В 3 т., Москва, 28-30 июня 2023 года. Том 2. М.: Издательство «Парадигма», 2023. С. 28-31.
6. Чозгиян О.П. Становление и развитие профессиональной позиции субъектности учителя начальных классов на примере организации спецкурса // Среднее профессиональное образование. 2013. №11. С. 35-37.

Formation of cognitive interest in oral calculations among younger schoolchildren in a mathematics lesson through the organization of various types of mathematical warm-up

Guskova A.А.,
student of 3 course of the Moscow City University, Moscow

Research supervisor:
Nekrashevich Olga Alexandrovna,
Teacher of the Department of Pedagogy and Methods of Primary General Education of the Institute of Secondary Vocational Education named after K.D. Ushinsky of the Moscow City University

Annotation. The article is devoted to the problem of formation of cognitive interest in oral calculations among younger schoolchildren at mathematics lessons. The types of mathematical warm-ups are considered. Own system of mathematical warm-up have been developed for program of first grade.
Keywords: oral calculations, mathematical warm-up.

Literature:

1. Bantova MA, Beltyukova G.V. Methods of teaching mathematics in primary grades. Moscow: Enlightenment, 2004. 335 pages.
2. Gavrilina O.V. The principle of an individual approach in the process of forming computational skills among younger schoolchildren // Bulletin of the Belgorod Institute for the Development of Education. 2018. 139 pages.
3. Tregubova N.E. Activating the cognitive activity of younger schoolchildren in mathematics lessons // Young scientist. 2014. №18(77). Page: 652-655.
4. Chozgiyan H.P. Transition to educational standards of primary general education of a new generation: current problems of updating approaches to education at the preschool level // Preschooler. Methodology and practice of upbringing and training. 2023. №1. Page: 3-9.
5. Chozgiyan H.P. Development of awareness of the adoption of a professional position among future teachers (level - SPO ) // The Big Conference of the Moscow State Pedagogical University: a collection of theses. In 3 tons, Moscow, June 28-30, 2023. Volume 2. Moscow: Paradigm Publishing House, 2023. Page: 28-31.
6. Chozgiyan H.P. Establishment and development of the professional position of a primary school teacher on the example of organizing a special course // Secondary vocational education. 2013. №11. Page: 35-37.