Аннотация. В данной статье представлены методические особенности изучения курса тригонометрии в рамках курса Геометрия 7-9. Ключевая идея статьи состоит в следующем: на примере геометрических задач, направленных на осуществление пропедевтики темы «Тригонометрические тождества», продемонстрировать возможности создания проблемных ситуаций и различные приемы мотивации обучающихся на уроках геометрии в 8-9 классах.
Ключевые слова: Методика обучения математике, создание проблемных ситуаций на уроках геометрии, тригонометрия в курсе геометрии.
Традиционно в курсе «Алгебра и начала математического анализа 10-11 класс» доказательства многих тригонометрических тождеств (в их числе формулы тригонометрических функций двойного угла, тригонометрических функций суммы и разности двух углов и другие) производятся путем цепочки тождественных преобразований практически без опоры на геометрические конструкции. Между тем, геометрические представления тригонометрических формул дают наглядность, которая является одним из основных критериев их запоминания.
Более того, рассмотрение тригонометрических тождеств в курсе геометрии восьмого класса, во-первых, знакомит обучающихся с тригонометрическими тождествами на пропедевтическом уровне (необходимо обратить внимание на ограничение градусной меры угла), во-вторых, повышает познавательную активность и активизирует исследовательский интерес учеников, и, в-третьих, дает дополнительные инструменты для решения задач.
Также стоит отметить, что интеграция темы «Тригонометрические тождества» в процесс обучения геометрии дает дополнительные возможности для развития навыков исследовательской и проектной деятельности, что на данный момент является одной из задач, которые ФГОС ставит перед школой.
Данная тема находит свое отражение в некоторых учебниках: например, в учебниках «Математическая вертикаль» эта тема рассматривается на ряду с другими, однако и в классах, в которых ученики осваивают программу на базовом уровне, будет полезно осветить данный материал по вышеперечисленным причинам.
Таким образом, целью данной работы является разработка приемов мотивации учащихся к исследовательской и проектной деятельности посредством проблемных задач по теме «Тригонометрические тождества».
Перейдем к рассмотрению конкретных примеров задач.

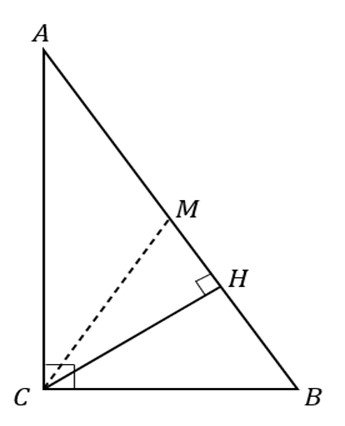

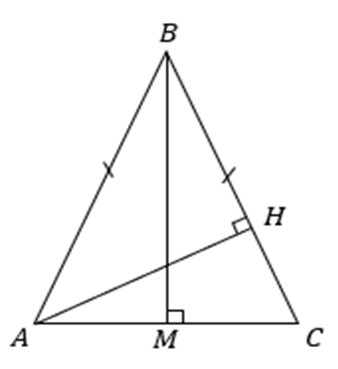


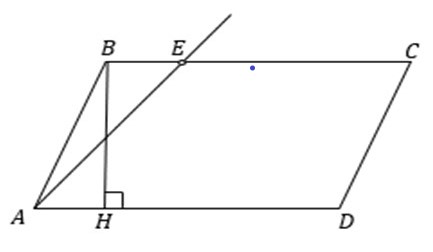

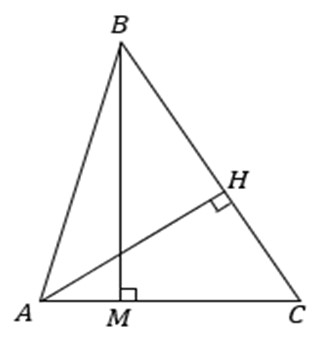

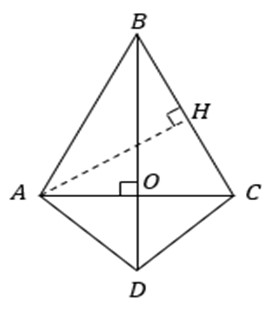

Выводы. Интеграция в процесс обучения геометрии темы «Тригонометрические тождества» посредством решения проблемных задач помимо очевидной пропедевтики данной темы открывает новые возможности для исследовательской и проектной деятельности обучающихся, при этом исследовательский интерес, помимо всего прочего, подкрепляется новизной этой темы.
Примечание. Все задачи, предложенные в настоящей работе, являются авторскими и разработаны соавторами данной статьи, как и доказательства теорем 1-3.
Литература:
- Алексеев Н.Г. Концепция развития исследовательской деятельности учащихся. / Н.Г. Алексеев, А.В. Леонтович, А.С. Обухов, Л.Ф. Фомина // Исследовательская работа школьников. 2002. №1. С. 24-33.
- Биянова Е.Б. Педагогические условия организации исследовательской деятельности учащихся основной школы: автореф. дис. канд. пед. наук: 13.00.02 / Е.Б. Биянова; Глазов. гос. пед. ун-т. Ижевск, 2011. 23 с.
- Геометрия. 7-9 классы: учеб. для общеобразоват. организаций с прил. на электрон. носителе / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. 3-е изд. М.: Просвещение, 2014. 383 с.
- Далингер В.А. Поисково-исследовательская деятельность учащихся по математике: Учебное пособие. Омск: Изд-во ОмГПУ, 2005. 456 с.
- Мадер В.В. Полифония доказательств: учеб. пособие. М.: Мнемозина, 2009. 344 с.
- Теория и методика обучения математике в школе. Часть 1. Учебно-методическое пособие для студентов математического факультета по специальности 050202.65 (032100) – математика / Авторы-сост.: Л.О. Денищева, А.Е. Захарова, М.Н. Кочагина, Н.В. Савинцева, Н.Е. Федорова. М.: МГПУ, 2008. 190 с.
Geometric representations of trigonometric identities as a tool for creating problem situations
Savvateev D.A.
bachelor of 3 course of the Moscow City University, Moscow
Coauthor:
Moshenina E.D.
bachelor of 3 course of the Moscow City University, Moscow
Research supervisor:
Zaharova Tatiana Alekseevna
Assistant of the Department of Mathematics and Physics of the Institute of Digital Education of the Moscow City University
Annotation. This article presents the methodological features of studying the course of trigonometry in the course of Geometry 7-9. The key idea of the article is as follows: using the example of geometric problems aimed at implementing the propaedeutics of the topic «Trigonometric identities», to demonstrate the possibilities of creating problem situations and various methods of motivating students in geometry lessons in grades 8-9.
Keywords: Methods of teaching mathematics, creating problem situations in geometry lessons, trigonometry in geometry course.
Literature:
- Alekseev N. The concept of the development of students' research activities. / N.G. Alekseev, A.V. Leontovich, A.S. Obukhov, L.F. Fomina // Research work of schoolchildren. 2002. № 1. Page: 24-33.
- Biyanova E. Pedagogical conditions for the organization of research activities of primary school students: abstract. dis. candidate of Pedagogical Sciences: 13.00.02 / E.B. Biyanova; Glazov. gos. ped. un-T. Izhevsk, 2011. 23 pages.
- Grades 7-9: studies. for general education. organizations with adj. on the electron. / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev, etc. 3rd ed. Moscow: Prosveshchenie, 2014. 383 pages.
- Dalinger V. Search and research activity of students in mathematics: Study guide. Omsk: Publishing House of OmSPU, 2005. 456 pages.
- Mader V. Polyphony of proofs: textbook. manual. Moscow: Mnemosyne, 2009. 344 pages.
- Theory and methodology of teaching mathematics at school. Part 1. Educational and methodological manual for students of the Faculty of Mathematics in the specialty 050202.65 (032100) – mathematics / Authors-comp.: L.O. Denishcheva, A.E. Zakharova, M.N. Kochagina, N.V. Savintseva, N.E. Fedorova. Moscow: MCU, 2008. 190 pages.
