Аннотация. В статье рассматривается влияние задач, основанных на анализе готовых геометрических чертежей, на формирование пространственных представлений у обучающихся в процессе изучения курса планиметрии на уровне основного общего образования. Анализируется теоретическое значение пространственного мышления в обучении геометрии, подчёркивается роль задач с визуальной опорой в развитии аналитического и наглядно-образного мышления. Приводятся примеры задач, раскрывающие возможности применения готовых чертежей для формирования устойчивых пространственных представлений обучающихся 7-9 классов. Сделаны выводы о высокой педагогической эффективности данного подхода в условиях современного школьного образования.
Ключевые слова: планиметрия, пространственное мышление, геометрия, задачи на готовых чертежах, визуальное мышление, методика обучения, основное общее образование.
В условиях современной образовательной среды, ориентированной на развитие универсальных учебных действий и метапредметных компетенций, особое значение приобретает формирование пространственных представлений у обучающихся. Пространственное мышление – это важный компонент когнитивной сферы, обеспечивающий успешное усвоение не только математических знаний, но и основ инженерных, архитектурных, технических и естественнонаучных дисциплин [2]. Развитие этих навыков начинается задолго до изучения пространственных тел и решения стереометрических задач в старшей школе. Уже на уровне основного общего образования, в частности при изучении курса планиметрии в 7-9 классах, закладываются основы пространственного восприятия, формируется умение интерпретировать геометрические образы и выполнять операции в воображаемом пространстве [6].
Планиметрический материал представляет собой фундаментальную основу для формирования пространственных представлений у обучающихся. Отметим, что работа с геометрическими чертежами на плоскости требует от учащегося способности мысленно «видеть» фигуры в движении, представлять их преобразования, устанавливать взаимосвязи между элементами геометрических форм и фигур [3]. Одним из эффективных дидактических приёмов, способствующих активному включению этих процессов, являются задачи на готовых чертежах. В отличие от традиционных заданий, в которых обучающимся предлагается самостоятельно построить изображение, такие задачи направлены на анализ уже представленной геометрической конструкции. Это позволяет сместить акцент с технических навыков построения на развитие аналитических способностей, визуального восприятия, логики и пространственного воображения.
Задачи на готовых чертежах предполагают анализ уже предложенной графической модели и требуют от учащегося интерпретации изображенного, а не воспроизведения. Такие задачи могут включать [1]; [4]; [5]:
- определение геометрических характеристик (длина, угол, площадь);
- нахождение взаимного расположения элементов;
- выявление скрытых элементов (например, выполнение необходимых дополнительных построений);
- ментальное преобразование объекта (поворот, отражение).
Пример 1. Дан треугольник RMN. Используя данные чертежа, определите градусную величину угла MON [1].
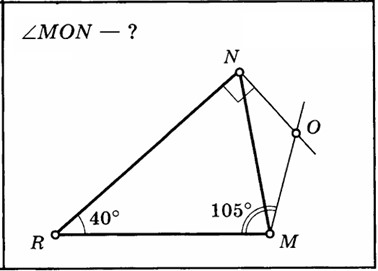
Рис. 1.1. Задача 32. Таблица 9 «Углы треугольника» [1]
Данная задача требует пространственного восприятия чертежа и умения соотнести изображённое с теоретическими знаниями. Учащийся должен не просто вычислить угол, а проанализировать структуру треугольника. Решение данной задачи целесообразно начинать с определения данных условий: ∠R = 40°, ∠RMO = 105°, ∠RNO – прямой, а значит, его величина составляет 90°.
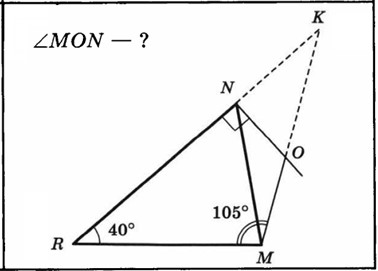
Рис. 1.2. Задача 32. Таблица 9 «Углы треугольника» [1]
Продолжим RN и MO до пересечения в точке К. Так как ∠R = 40°, ∠RMO = 105°, то ∠К = 180° – (40° + 105°) = 35° (по теореме о сумме углов треугольника). По условию RN ⊥ NO, тогда внешний угол MON треугольника KON будет равен: ∠MON = ∠К + ∠ONK = 35° + 90° = 125°.
Ответ: 125°.
Особую ценность задачи на готовых чертежах приобретают в условиях массового образования, где уровень обучающихся может значительно различаться. Такие задания позволяют дифференцировать подход к обучению, варьировать сложность задач с учётом типа мышления, который они активизируют. Более того, готовый чертёж снимает часть когнитивной нагрузки, позволяя сосредоточиться на осмыслении взаимосвязей между геометрическими элементами, их свойств и преобразований. Визуальный образ становится не просто иллюстрацией, а полноценным объектом исследования, требующим внимательного анализа и логического осмысления [3].
Значительная часть трудностей, которые испытывают учащиеся при переходе к изучению объемных тел, связана с тем, что на этапе планиметрии внимание чаще всего акцентируется на вычислениях и техническом воспроизведении чертежей, в то время как развитие пространственного мышления требует анализа, рассуждения и работы с готовой геометрической моделью. Именно в этом контексте особую методическую ценность приобретают задачи, в которых чертёж уже представлен.
Ещё один интересный с методической точки зрения тип задач связан с нахождением и доказательством равенства или подобия фигур. Несмотря на простоту формулировки, для успешного решения требуется мысленно наложить одну фигуру на другую, представить совпадение их элементов, что активизирует пространственное мышление.
Пример 2. Укажите подобные треугольники и докажите их подобие [5].
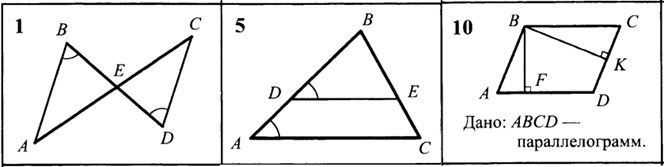
Рис. 2. Задачи 1, 5, 10. Таблица 9.2 «Первый признак подобия треугольников» [5]
Определение и доказательство подобия треугольников требует серьёзной математической подготовки обучающихся, твёрдых геометрических знаний и гибкости образного мышления. Так, при выполнении задачи 1 необходимо вспомнить свойство вертикальных углов, тогда ∠AEB = ∠DEC, а значит, треугольники AEB и DEC подобны по двум равным углам. При решении задачи 5 обучающимся следует заметить равенство углов CAB и EDB и общий угол В для треугольников ABC и DBE, подобных по двум равным углам. Большую сложность представляет задача 10. Заметим, что по свойству противоположных углов параллелограмма угол BAF и угол BCK будут равны – это первое необходимое условие для доказательства подобия треугольников. Кроме того, BF ⊥ AD и BK ⊥ CD, тогда ∠BFA = ∠BKC = 90°. Значит, треугольники BFA и BKC подобны так же по двум равным углам.
Задачи на готовых чертежах предполагают, что учащийся не тратит усилия на построение изображения, а сосредотачивает внимание на его анализе. Это не означает, что такие задания проще – напротив, они часто сложнее, так как требуют большей абстракции, умения выявлять закономерности, находить неочевидные связи и проводить логические рассуждения на основе зрительной информации. Такие задания способствуют развитию зрительного внимания, пространственного воображения, аналитических и синтетических операций мышления. Учащиеся учатся интерпретировать чертёж как информационный ресурс, вычленять из него существенные элементы, соотносить геометрические свойства и делать закономерные выводы.
Этап поиска решения в задачах на готовых чертежах представляет собой особую когнитивную активность, направленную на установление логических связей между элементами изображения, выявление закономерностей и формирование гипотез, которые могут привести к верному ответу [2]. В отличие от задач, требующих построения фигуры, здесь ученик сталкивается с уже заданной геометрической ситуацией, которую необходимо осмыслить, интерпретировать и «раскрыть» как логическую структуру.
Первым шагом на этом этапе является визуальное сканирование чертежа, в ходе которого обучающийся определяет известные элементы: стороны, углы, отрезки, точки пересечения, оси симметрии и иные признаки. Это требует умения внимательно и избирательно воспринимать информацию, концентрируя внимание на значимых деталях.
Следующий шаг – актуализация знаний. Обучающийся вспоминает геометрические свойства фигур, теоремы и определения, которые могут быть применимы к данной ситуации. Например, при виде параллельных отрезков или углов, образованных при пересечении прямых, он обращается к знаниям о признаках равенства или подобия треугольников, свойствах углов при параллельных прямых. На этом этапе задействуется логико-дедуктивное мышление и умение соотнести абстрактные понятия с конкретной ситуацией на чертеже [6].
Затем наступает момент моделирования и гипотезирования. Ученик формулирует возможные пути решения: предположения о равенстве углов, равенстве сторон, параллельности, соотношениях между отрезками и т.д. Эти предположения основываются как на визуальном анализе, так и на интуитивном пространственном восприятии. На этапе выбора стратегии решения ученик оценивает целесообразность различных подходов: доказательство через подобие, использование теорем о смежных и вертикальных углах, применение тригонометрических зависимостей, поиск вспомогательных построений. Несмотря на то, что чертёж уже дан, он может дополняться мысленно – в воображении учащегося или непосредственно на бумаге.
Пример 3. Дана трапеция ABCD, у которой основания AD и BC равны 32 и 16 соответственно. Найдите площадь данной трапеции [1].
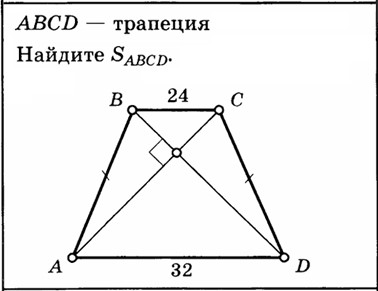
Рис. 3.1. Задача 19. Таблица 11 «Площадь трапеции» [1]
Выполнив анализ чертежа и определив достаточные и необходимые условия для решения задачи, обучающиеся могут сделать вывод, что ABCD – равнобедренная трапеция с равными боковыми сторонами AB и CD, а её диагонали AC и BD перпендикулярны. Следующий этап – поиск решения. Необходимо вспомнить о типовых конструкциях планиметрии при решении задач с данным видом трапеции: дополнительное построение высот трапеции, её средней линии или прямых, параллельных боковым сторонам или диагоналям.
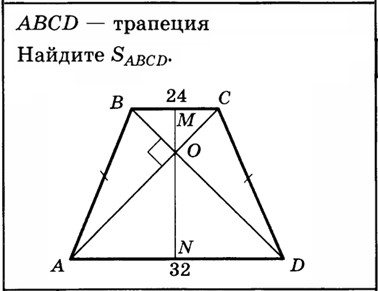
Рис. 3.2. Задача 19. Таблица 11 «Площадь трапеции» [1]
Сделаем дополнительное построение и проведём высоту MN трапеции через точку пересечения диагоналей AC и BD. Так как по условию AB = CD и AC ⊥ BD, то AD = 2·ON и BC = 2·OM, тогда:
По условию задачи AD = 32, BC = 24, тогда ON = ·AD = 16, OM = · BC = 12. Значит, MN = ON + OM = 16 + 12 = 28, тогда
Ответ: 784.
Отметим, что при решении данной задачи обучающиеся также доказали, что «если в равнобедренной трапеции диагонали перпендикулярны, то площадь и , где – высота трапеции, и – основания».
Проведённый анализ позволяет с уверенностью утверждать, что задачи на готовых чертежах играют важную роль в формировании и развитии пространственных представлений обучающихся в рамках курса планиметрии на уровне основного общего образования. В отличие от задач с обязательным построением, подобные задания создают условия для более глубокого погружения в логико-геометрический анализ и развивают способность интерпретировать визуальную информацию как источник теоретических и практических знаний.
Такие задачи активизируют разные виды мышления: наглядно-образное, пространственное, логическое, аналитическое. Работа с готовым изображением способствует развитию умений выделять ключевые элементы геометрической конфигурации, устанавливать взаимосвязи между ними, использовать геометрические свойства фигур в нестандартных ситуациях [3]. Учащийся начинает воспринимать чертёж как объект исследования, а не только как вспомогательное средство.
Кроме того, задачи на готовых чертежах обеспечивают более высокий уровень вовлечённости обучающихся в учебный процесс. Они способствуют формированию исследовательского подхода к решению задач, мотивируют к самостоятельному поиску решений, развивают умения выдвигать и проверять гипотезы. Особенно важно то, что данные задания позволяют варьировать уровень сложности и адаптировать задания под разные типы учеников, что делает их эффективным инструментом в условиях дифференцированного и личностно-ориентированного обучения.
В методическом плане задачи на готовых чертежах открывают широкие возможности для построения развивающей образовательной среды [2]. Их можно использовать не только в рамках урока, но и во внеурочной деятельности, на олимпиадах, математических кружках, в дистанционном обучении. Они способствуют формированию метапредметных навыков, таких как умение анализировать, моделировать, делать обоснованные выводы и представлять информацию в различных формах.
Таким образом, задачи на готовых чертежах – это не просто разновидность заданий в курсе геометрии, а мощное дидактическое средство, позволяющее формировать у школьников прочные и гибкие пространственные представления, необходимые как для дальнейшего изучения математики, так и для общего интеллектуального развития.
Список литературы:
- Балаян Э.Н. Геометрия: задачи на готовых чертежах для подготовки к ГИА и ЕГЭ: 7-9 классы. Изд. 5-е, исправл. и дополн. Ростов н/Д: Феникс, 2013. 223 с.
- Далингер В.А. Методика обучения математике. Поисково-исследовательская деятельность учащихся: учебник и практикум для вузов. 2-е изд., испр. и доп. М.: Издательство Юрайт, 2025. 460 с.
- Крымская Ю.А., Ячинова С.Н. Роль упражнений на готовых чертежах в процессе обучения решению геометрических задач // Молодой ученый, 2014. №17(76). С. 498-501.
- Орехова А.И. Задачи на готовых чертежах. Геометрия: в 3 ч. Ч. 1. 4-е изд. Мозырь: Белый Ветер, 2011. 45 с.
- Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия. М.: ИЛЕКСА, 2016. 60 с.
- Титова Е.И., Чапрасова А.В., Ячинова С.Н. Формирование умений работы с чертежом в процессе решения геометрических задач // Современные проблемы науки и образования, 2014. №2. С. 269.
Tasks on ready-made drawings and their influence on the formation of spatial representations of students at the level of basic general education
Vishnevskii V.A.,
student of 4 course of the Moscow City University, teacher of mathematics, School «Pokrovskiy kvartal», Moscow
Coauthor:
Melnikova R.R.,
teacher of mathematics and computer science, School «Pokrovskiy kvartal», Moscow
Abstract. The article deals with the influence of tasks based on the analysis of ready-made geometric drawings on the formation of spatial representations in students in the process of studying the course of planimetry at the level of basic general education. The theoretical importance of spatial thinking in teaching geometry is analysed, the role of tasks with visual support in the development of analytical and visual imaginative thinking is emphasized. Examples of tasks revealing the possibilities of using ready-made drawings for the formation of stable spatial representations of students of 7-9 grades are given. Conclusions about high pedagogical efficiency of this approach in the conditions of modern school education are drawn.
Keywords: planimetry, spatial thinking, geometry, tasks on ready-made drawings, visual thinking, teaching methodology, basic general education.
References:
- Balayan E.N. Geometry: tasks on ready-made drawings for preparation for the GIA and the Unified State Exam: grades 7-9. 5th ed., corrected. and the add-on. Rostov n/A: Phoenix, 2013. 223 p.
- Dalinger V.A. Methods of teaching mathematics. Search and research activities of students: a textbook and a workshop for universities. 2nd ed., ispr. and add. Moscow: Yurayt Publishing House, 2025. 460 p.
- Krymskaya Yu.A., Yachinova S.N. The role of exercises on ready-made drawings in the learning process of solving geometric problems. Young scientist, №17(76).: 498-501.
- Orekhova A.I. Tasks on ready-made drawings. Geometry: at 3 o'clock in 1. 4th ed. Mozyr: White Wind, 2011. 45 p.
- Rabinovich E.M. Tasks and exercises on ready-made drawings. Grades 7-9. Geometry. Moscow: ILEX, 2016. 60 p.
- Titova E.I., Chaprasova A.V., Yachinova S.N. Formation of skills of working with a drawing in the process of solving geometric problems // Modern problems of science and education, 2014. №2.: 269.
